Beleuchtung
Storyboard 
Nachdem die natürliche Beleuchtung bewertet wurde, kann man feststellen, wie viel zusätzliches Licht tagsüber benötigt wird, und das Beleuchtungssystem entsprechend gestalten. Außerdem ist es wichtig, die erforderliche Beleuchtungsmenge für Zeiten zu berechnen, in denen kein Tageslicht verfügbar ist.
ID:(2093, 0)
Photonengasmodell
Konzept 
Ein einfaches Modell zur Untersuchung der erforderlichen Beleuchtung ist das eines Photonengases, das das Volumen des Raumes einnimmt. Diese Teilchen gelangen durch die Fenster von außen und/oder durch Lampen im Raum in den Raum:
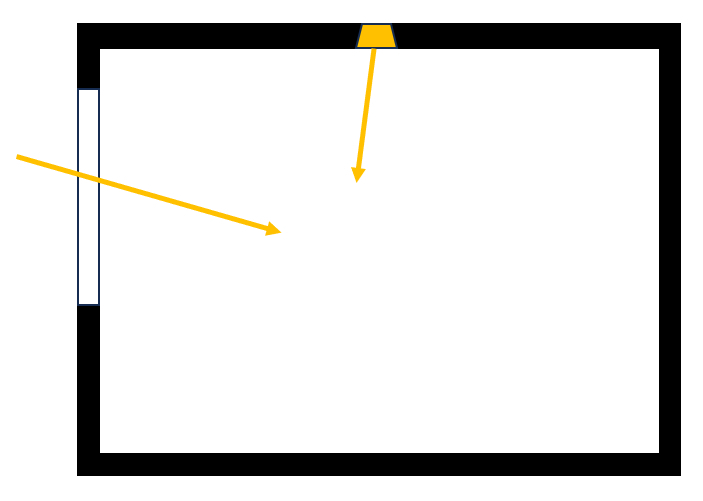
None
Die Photonen bewegen sich mit die Lichtgeschwindigkeit ($c$) durch den Raum, prallen gegen die Wände, wobei nur ein Bruchteil entsprechend der Albedo ($a$) reflektiert wird. Der Bruchteil $1-a$ wird von den Wänden absorbiert, und die Photonen verlassen somit das System:
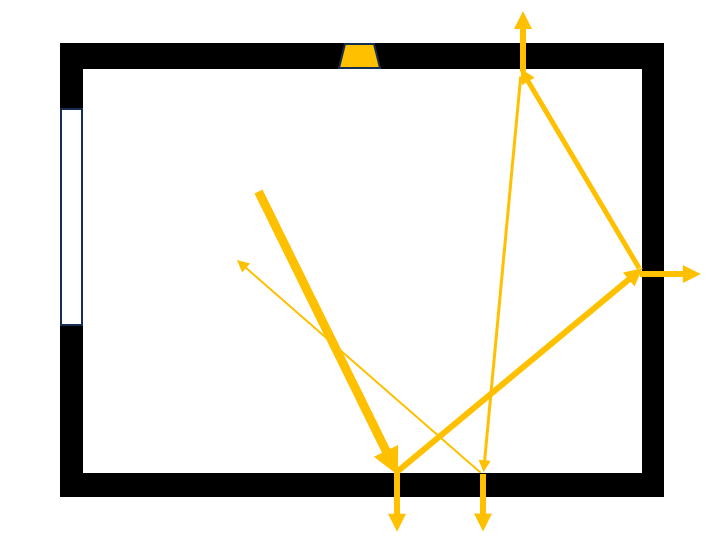
Da die Wände nicht vollkommen glatt sind, reflektiert das Licht isotrop, also ohne eine bestimmte Richtung zu bevorzugen. Am Ende gibt es einen einfallenden Photonenfluss durch die Fenster und/oder Lampen sowie einen dominanten Absorptionsfluss an den Wänden, der sich in einer stationären Situation dem einfallenden Fluss anpasst:
ID:(137, 0)
Referenzphotonenkonzentration
Konzept 
Die Menge des Lichts, dargestellt durch die Anzahl der Photonen, die pro Zeiteinheit in den Raum eindringen, sei es durch Fenster oder Lampen, kann mit den Variablen die Intensität ($I$) und Fläche der Quelle ($S_w$) geschätzt werden, wobei jedes Photon eine Energie von die Photon energy ($\epsilon$) besitzt. Diese Beziehung wird durch die folgende Formel dargestellt:
$\displaystyle\frac{I S_w}{\epsilon}$
Diese ist in der folgenden Grafik dargestellt:
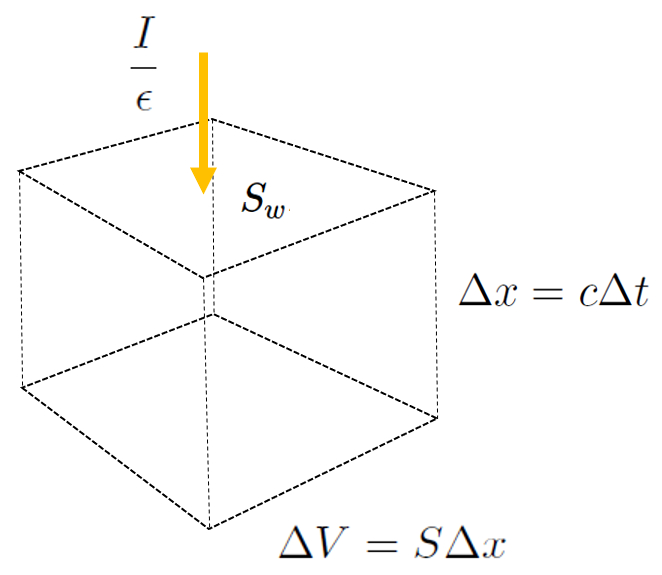
Die Photonen, die in den Raum eindringen, gehen durch Absorption an den Oberflächen von Wänden, Decke und Boden verloren, entsprechend dem Wert Wandflächen ($S$). Die Anzahl der Photonen, die diese Oberflächen treffen, ist proportional zu die Photonenkonzentration ($n$), und der absorbierte Bruchteil ist das Komplement von der Albedo ($a$). Wenn die Verteilung der Photonen anisotrop ist, werden nur 1/6 der Photonen in der Nähe der Oberfläche in Richtung der Oberfläche reisen. Daher kann der Fluss der absorbierten Photonen ausgedrückt werden als:
$\displaystyle\frac{1}{6} n S (1-a)$
Diese Beziehung wird ebenfalls in der folgenden Grafik dargestellt:
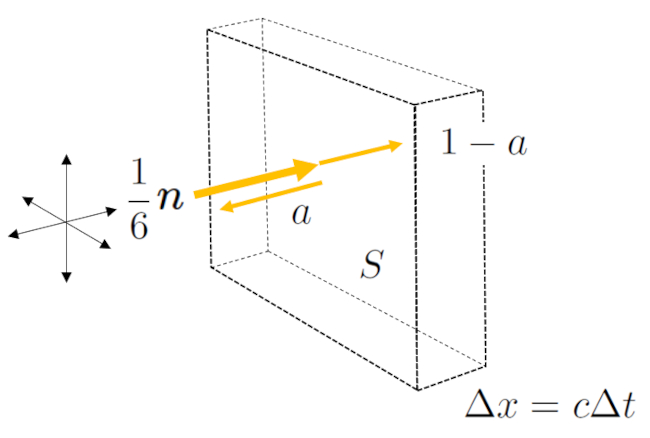
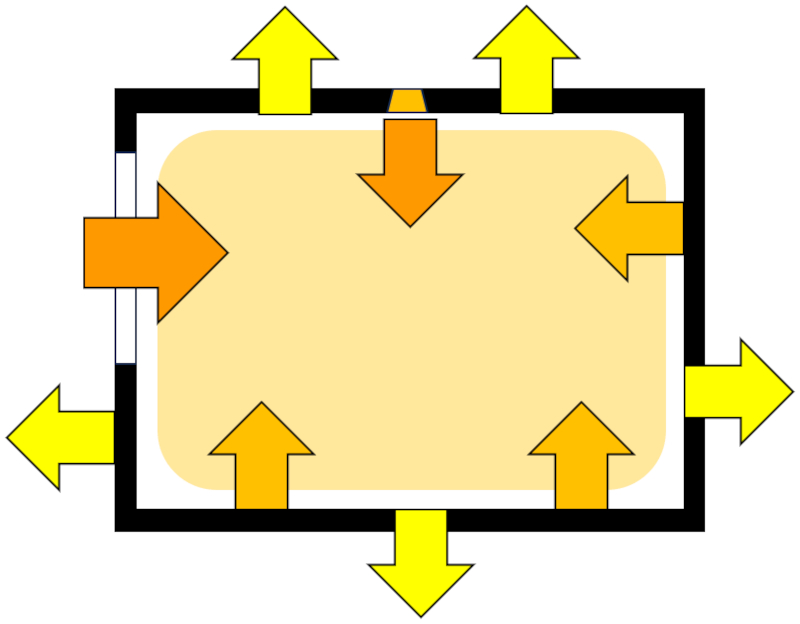
Im Allgemeinen ist der zweite Fluss kleiner als der erste, was bedeutet, dass der einfallende Fluss durch mehrere Reflexionen an den Wänden absorbiert wird. Dieser Prozess ist jedoch so schnell, dass das menschliche Auge ihn nicht wahrnehmen kann, sodass die Unterbrechung einer Lichtquelle zu einer scheinbar sofortigen Verdunkelung führt.
ID:(139, 0)
Photonengleichgewicht
Konzept 
Unter Berücksichtigung des einfallenden und des absorbierten Photonflusses lässt sich berechnen, wie die Photonenkonzentration ($n$) in Abhängigkeit von der Zeit ($t$) in Raumvolumen ($V$) variiert. Dies wird im folgenden Diagramm dargestellt:

Es zeigt, dass die Änderung von die Photonenkonzentration ($n$) in Bezug auf der Zeit ($t$),
$\displaystyle\frac{dn}{dt}$
gleich dem einfallenden Fluss ist:
$\displaystyle\frac{S_w I}{\epsilon V}$
mit den Variablen Fläche der Quelle ($S_w$), die Intensität ($I$), die Photon energy ($\epsilon$) und Raumvolumen ($V$), abzüglich des Verlustes durch Absorption an den Wänden:
$\displaystyle\frac{1}{6}\displaystyle\frac{S (1-a) c n}{V}$
unter Verwendung der Variablen die Lichtgeschwindigkeit ($c$), der Albedo ($a$) und Wandflächen ($S$), was zu folgender Gleichung führt:
| $\displaystyle\frac{ dn }{ dt } = -\displaystyle\frac{1}{6} c \displaystyle\frac{ S }{ V }(1-a) n + \displaystyle\frac{ S_w I }{ \epsilon V }$ |
ID:(15869, 0)
Modell
Top 
Parameter
Variablen
Berechnungen
Berechnungen
Berechnungen
Gleichungen
$ c = \nu \lambda $
c = nu * lambda
$ \epsilon = h \nu $
e = h * nu
$ n = n_a + (n_0 - n_a) e^{- t / \tau }$
n = n_a +( n_0 - n_a )*exp(- t / tau )
$ n_a = \displaystyle\frac{6 I }{ c (1- a )\epsilon}\displaystyle\frac{ S_w }{ S }$
n_a = 6 * I * S_w /( c *(1- a )* e * S )
$ \tau = \displaystyle\frac{ 6 V }{ c (1- a ) S }$
tau = 6* V /( c *(1 - a )* S )
$\displaystyle\frac{ dn }{ dt } = -\displaystyle\frac{1}{6} c \displaystyle\frac{ S }{ V }(1-a) n + \displaystyle\frac{ S_w I }{ \epsilon V }$
@DIF( n , t , 1) = - c * S *(1- a ) * n /(6* V ) + S_w * I /( e * V )
ID:(15874, 0)
Photonengleichgewicht
Gleichung 
Die Variation von die Photonenkonzentration ($n$) in Abhängigkeit von der Zeit ($t$) ergibt sich aus dem einströmenden Fluss abzüglich des Anteils, der absorbiert wird. Daher erhält man unter Verwendung der Variablen Fläche der Quelle ($S_w$), die Intensität ($I$), Wandflächen ($S$), der Albedo ($a$), Raumvolumen ($V$), die Lichtgeschwindigkeit ($c$) und die Photon energy ($\epsilon$) die folgende Gleichung:
Die Variation von die Photonenkonzentration ($n$) in Bezug auf der Zeit ($t$),
$\displaystyle\frac{dn}{dt}$
wird dem einfallenden Fluss entsprechen:
$\displaystyle\frac{S_w I}{\epsilon V}$
wobei die Variablen Fläche der Quelle ($S_w$), die Intensität ($I$), die Photon energy ($\epsilon$) und Raumvolumen ($V$) verwendet werden, abzüglich des Verlusts durch Absorption an den Wänden:
$\displaystyle\frac{1}{6}\displaystyle\frac{S (1-a) c n}{V}$
unter Verwendung der Variablen die Lichtgeschwindigkeit ($c$), der Albedo ($a$) und Wandflächen ($S$), was zu folgender Gleichung führt:
| $\displaystyle\frac{ dn }{ dt } = -\displaystyle\frac{1}{6} c \displaystyle\frac{ S }{ V }(1-a) n + \displaystyle\frac{ S_w I }{ \epsilon V }$ |
ID:(15870, 0)
Frequenz und Wellenlänge von Photon
Gleichung 
Das Photon wird als Welle beschrieben, und der Photon Frequency ($\nu$) steht in Beziehung zu ($$) durch die Lichtgeschwindigkeit ($c$), gemäß der folgenden Formel:
Da die Frequenz das Reziprokum der Zeit für eine Schwingung ist:
$\nu=\displaystyle\frac{1}{T}$
bedeutet dies, dass die Lichtgeschwindigkeit gleich der Strecke ist, die in einer Schwingung zurückgelegt wird, das ist die Wellenlänge, geteilt durch die benötigte Zeit, das ist die Periode:
$c=\displaystyle\frac{\lambda}{T}$
Mit anderen Worten:
| $ c = \nu \lambda $ |
Diese Formel entspricht der mechanischen Beziehung, die besagt, dass die Wellengeschwindigkeit gleich der Wellenlänge (zurückgelegte Strecke) geteilt durch die Schwingungsperiode ist, oder umgekehrt proportional zur Frequenz (dem Kehrwert der Periode).
ID:(3953, 0)
Photon Energie
Gleichung 
Die Farbe des Lichts ist mit seiner der Photon Frequency ($\nu$) verbunden, und es gibt eine direkte Beziehung zwischen dieser Frequenz und die Photon energy ($\epsilon$):
wobei die Planck Konstante ($h$) einen Wert von $6,62\times 10^{-34} , \text{Js}$ hat.
ID:(3341, 0)
Photonenkonzentration im stationären Fall
Gleichung 
Im stationären Zustand ist die Anzahl der Photonen, die in den Raum eintreten, gleich der Anzahl der absorbierten Photonen. Das bedeutet, dass es eine die Asymptotische Photonenkonzentration ($n_a$) gibt, die mithilfe von Fläche der Quelle ($S_w$), die Intensität ($I$), Wandflächen ($S$), der Albedo ($a$), die Lichtgeschwindigkeit ($c$) und die Photon energy ($\epsilon$) berechnet werden kann, durch die folgende Gleichung:
Der Photonfluss in einem Raum wird durch die Photonenkonzentration ($n$) als Funktion von der Zeit ($t$) beschrieben, unter Verwendung der Variablen Fläche der Quelle ($S_w$), die Intensität ($I$), Wandflächen ($S$), der Albedo ($a$), die Lichtgeschwindigkeit ($c$) und die Photon energy ($\epsilon$), gemäß der folgenden Gleichung:
| $\displaystyle\frac{ dn }{ dt } = -\displaystyle\frac{1}{6} c \displaystyle\frac{ S }{ V }(1-a) n + \displaystyle\frac{ S_w I }{ \epsilon V }$ |
Im stationären Fall ist die Ableitung gleich null, und durch Umstellen der Gleichung für die Photonenkonzentration ($n$) lässt sich die Asymptotische Photonenkonzentration ($n_a$) mit der folgenden Beziehung definieren:
| $ n_a = \displaystyle\frac{6 I }{ c (1- a )\epsilon}\displaystyle\frac{ S_w }{ S }$ |
Es ist wichtig zu beachten, dass dies ein durchschnittliches Lichtniveau in einem Raum darstellt und je nach Standort im Raum variiert. Die Lichtintensität hängt davon ab, ob direktes Licht von der Quelle empfangen wird oder ob es durch mehrfache Reflexionen abgeschwächt wird. Diese Reflexionen nehmen allmählich ab und erzeugen Bereiche, in denen nur wenig Licht ankommt.
ID:(15868, 0)
Absorptionsentspannungszeit
Gleichung 
Mit der Photonbilanzgleichung und der stationären Photonenkonzentration lässt sich eine Zeitskala der Entspannungszeit ($\tau$) bestimmen, die von Raumvolumen ($V$), Wandflächen ($S$), der Albedo ($a$) und die Lichtgeschwindigkeit ($c$) abhängt, durch:
Da die Variation von die Photonenkonzentration ($n$) in Abhängigkeit von der Zeit ($t$) auf den einfallenden Fluss minus dem Anteil, der absorbiert wird, zurückzuführen ist, kann die Gleichung unter Verwendung der Variablen Fläche der Quelle ($S_w$), die Intensität ($I$), Wandflächen ($S$), der Albedo ($a$), Raumvolumen ($V$), die Lichtgeschwindigkeit ($c$) und die Photon energy ($\epsilon$) ausgedrückt werden, was zu folgender Gleichung führt:
| $\displaystyle\frac{ dn }{ dt } = -\displaystyle\frac{1}{6} c \displaystyle\frac{ S }{ V }(1-a) n + \displaystyle\frac{ S_w I }{ \epsilon V }$ |
Mit der Beziehung für die Asymptotische Photonenkonzentration ($n_a$) gegeben durch:
| $ n_a = \displaystyle\frac{6 I }{ c (1- a )\epsilon}\displaystyle\frac{ S_w }{ S }$ |
kann die Gleichung umgeschrieben werden als:
$\displaystyle\frac{dn}{dt} = \displaystyle\frac{1}{\tau}(n_0-n)$
wobei der Entspannungszeit ($\tau$) ist:
| $ \tau = \displaystyle\frac{ 6 V }{ c (1- a ) S }$ |
ID:(15872, 0)
Zeitliche Entwicklung der Photonenkonzentration
Gleichung 
Durch das Lösen der Photonenbilanzgleichung ergibt sich, dass die Photonenkonzentration ($n$) in Abhängigkeit von der Zeit ($t$), zusammen mit den Variablen der Anfangs Konzentration ($n_0$), die Asymptotische Photonenkonzentration ($n_a$) und der Entspannungszeit ($\tau$), ist:
Da die Variation von die Photonenkonzentration ($n$) in Abhängigkeit von der Zeit ($t$) auf den einfallenden Fluss abzüglich des absorbierten Anteils zurückzuführen ist, kann die Gleichung unter Verwendung der Variablen Fläche der Quelle ($S_w$), die Intensität ($I$), Wandflächen ($S$), der Albedo ($a$), Raumvolumen ($V$), die Lichtgeschwindigkeit ($c$) und die Photon energy ($\epsilon$) ausgedrückt werden, was zur folgenden Beziehung führt:
| $\displaystyle\frac{ dn }{ dt } = -\displaystyle\frac{1}{6} c \displaystyle\frac{ S }{ V }(1-a) n + \displaystyle\frac{ S_w I }{ \epsilon V }$ |
Mit der Beziehung für die Asymptotische Photonenkonzentration ($n_a$) gegeben durch:
| $ n_a = \displaystyle\frac{6 I }{ c (1- a )\epsilon}\displaystyle\frac{ S_w }{ S }$ |
und mit der Entspannungszeit ($\tau$):
| $ \tau = \displaystyle\frac{ 6 V }{ c (1- a ) S }$ |
kann die Gleichung umgeschrieben werden als:
$\displaystyle\frac{dn}{dt} = \displaystyle\frac{1}{\tau}(n_0-n)$
deren Lösung ist:
| $ n = n_a + (n_0 - n_a) e^{- t / \tau }$ |
mit der Anfangs Konzentration ($n_0$).
ID:(15871, 0)
