Utilizador:
Lei de Blondel
Descrição 
No século XVII, o arquiteto François Blondel [1] estudou a relação entre o la contrahuella ($h$) e o o piso ($d$) de uma escada para garantir que fosse confortável para o usuário.
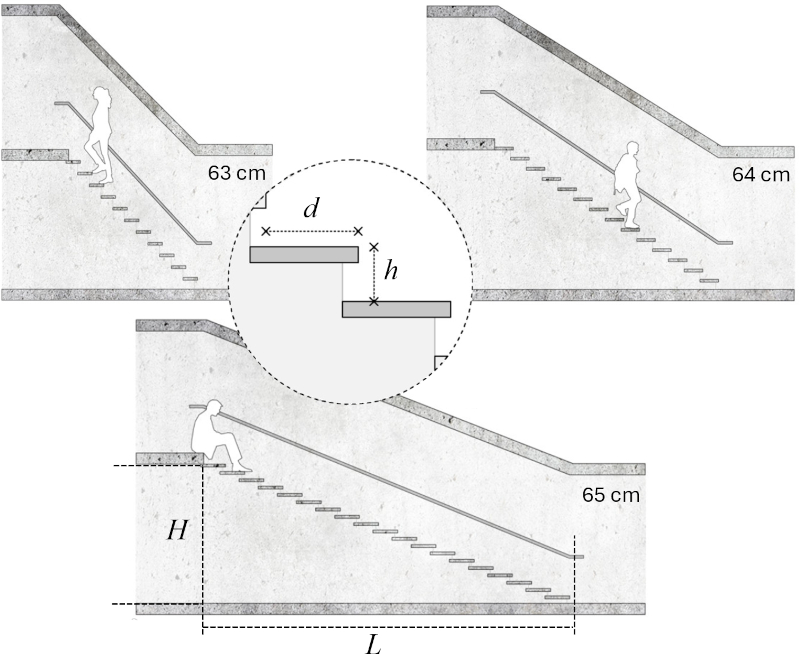
Ele descobriu que a relação deveria cumprir a seguinte equação:
| $2 h + d = c_2 $ |
onde la constante de Blondel (2) ($c_2$) deve estar entre 63 e 65 cm.
Para alcançar um maior conforto, também era necessário cumprir com la constante de Blondel (1) ($c_1$), que deveria ser da ordem de 46 cm, estabelecendo que a relação fosse:
| $h + d = c_1 $ |
[1] Cours dArchitecture, François Blondel, L'Académie Royale de Arquitecure, 1675
ID:(957, 0)
Número de degraus e comprimento da escada
Descrição
O número de etapas ($n$) depende de la altura da escada ($H$) e la contrahuella ($h$) pois representa o número de vezes que esta última cabe na altura total:
| $n = \displaystyle\frac{ H }{ h }$ |
Dado o piso ($d$), o comprimento da escada ($L$) pode ser calculado utilizando a seguinte fórmula:
| $ L = n d $ |
ID:(958, 0)
A escada em espiral
Descrição
Em uma escada em caracol com um diâmetro de o raio da escada ($R$), as pessoas caminham ao longo de um raio igual a o raio de caminhada ($r$):
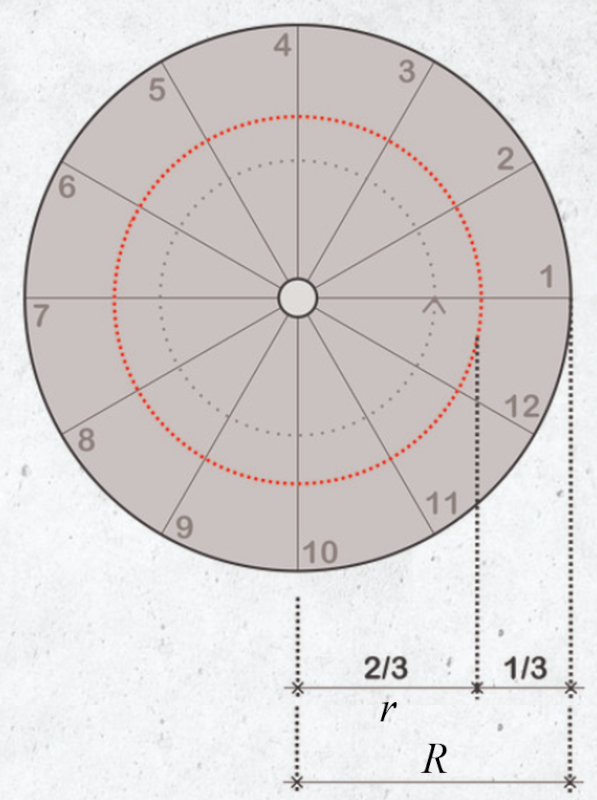
Este raio é calculado da seguinte maneira:
| $r = \displaystyle\frac{2 R }{3}$ |
Se o degrau for descrito como um elemento do círculo:
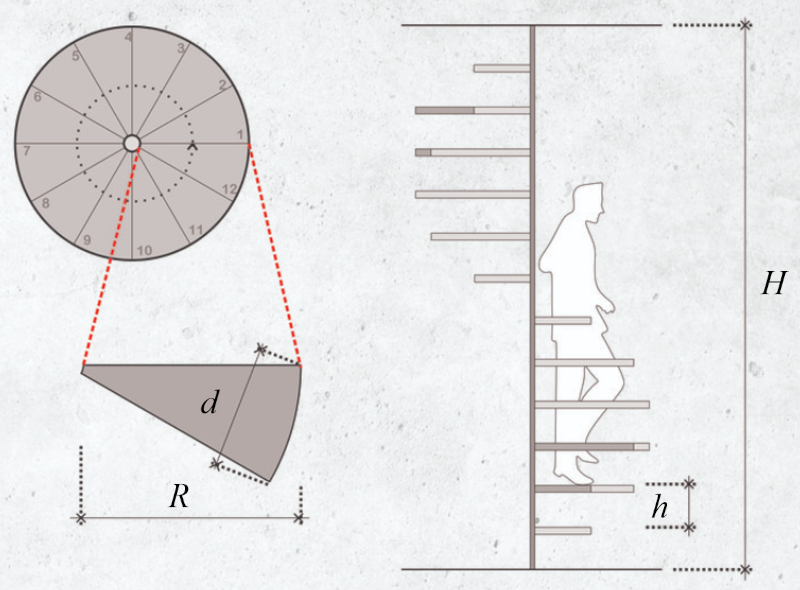
obtemos que o ângulo de passo ($\theta$) junto com o piso ($d$) é igual a:
| $ \theta = \displaystyle\frac{ d }{ r } $ |
Isso, por sua vez, define o volta completa ($\Omega$) através de:
| $ \Omega = n \theta $ |
ID:(959, 0)
Modelo
Descrição
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ L = n d $
L = n * d
$n = \displaystyle\frac{ H }{ h }$
n = H / h
$ \Omega = n \theta $
Omega = n * theta
$r = \displaystyle\frac{2 R }{3}$
r = 2* R /3
$ \theta = \displaystyle\frac{ d }{ r } $
theta = d / r
$2 h + d = c_2 $
2* h + d = c_2
$h + d = c_1 $
h + d = c_1
ID:(956, 0)
Lei de Blondel
Equação
No século XVII, o arquiteto François Blondel formulou a relação entre la contrahuella ($h$) e o piso ($d$) de uma escada para garantir seu conforto:
| $2 h + d = c_2 $ |
onde la constante de Blondel (2) ($c_2$) é aproximadamente 63 cm.
ID:(949, 0)
Segunda lei de Blondel
Equação
Existe uma segunda lei do arquiteto François Blondel que, para alcançar maior conforto, estabelece que a relação entre la contrahuella ($h$) e o piso ($d$) deve ser:
| $h + d = c_1 $ |
onde la constante de Blondel (1) ($c_1$) é aproximadamente 46 cm.
ID:(950, 0)
Número de etapas
Equação
Se la altura da escada ($H$) e la contrahuella ($h$) forem conhecidos, o número de etapas ($n$) pode ser calculado usando a seguinte fórmula:
| $n = \displaystyle\frac{ H }{ h }$ |
ID:(951, 0)
Raio de caminhada
Equação
Se o raio da escada ($R$) for conhecido, o raio de caminhada ($r$) pode ser calculado usando a seguinte fórmula:
| $r = \displaystyle\frac{2 R }{3}$ |
ID:(952, 0)
Comprimento da escada
Equação
O comprimento da escada ($L$) pode ser calculado a partir de o número de etapas ($n$) e o piso ($d$) usando a seguinte fórmula:
| $ L = n d $ |
ID:(953, 0)
Ângulo por passo
Equação
O ângulo de passo ($\theta$) pode ser calculado a partir de o piso ($d$), que corresponde ao arco, e de o raio de caminhada ($r$) usando a seguinte fórmula:
| $ \theta = \displaystyle\frac{ d }{ r } $ |
ID:(954, 0)
Volta completa
Equação
O volta completa ($\Omega$) é obtido a partir de o número de etapas ($n$) e o ângulo de passo ($\theta$) usando a seguinte fórmula:
| $ \Omega = n \theta $ |
ID:(955, 0)