Wasserbrunnen
Storyboard 
Wasserquellen umfassen Oberflächenquellen und gebohrte Brunnen. Bei Oberflächenquellen kann das Wasser direkt in einen Tank fließen und von dort aus verteilt werden. Bei gebohrten Brunnen muss das Wasser mit einer Pumpe gefördert und dann in den Tank geleitet werden, um es weiter zu verteilen.
ID:(144, 0)
In einen Brunnen fließen
Gleichung 
Wir können den stationären Fall analysieren, was impliziert, dass die Höhe der Wassersäule im Boden ($h$) geteilt durch die Flussdichte ($j_s$) konstant bleiben muss und insbesondere an einem bestimmten Punkt Werte annehmen kann, die durch die Referenzhöhe der Wassersäule ($h_0$) und den Fluss an einem Referenzpunkt ($j_{s0}$) dargestellt werden:
| $ h j_s = h_0 j_{s0} $ |
repräsentiert, was das Wasserprofil im Boden definiert:
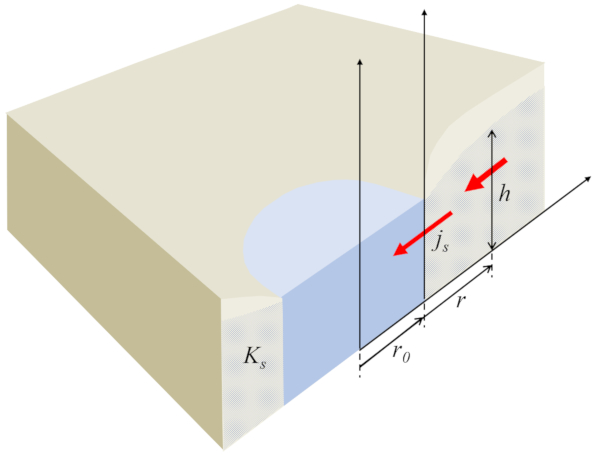
ID:(882, 0)
Fließhöhenlösung in Richtung eines Brunnens
Gleichung 
Die Lösung der eindimensionalen Fließgleichung zu einem Brunnen, bei der die Höhe der Wassersäule im Boden ($h$) in Abhängigkeit vom Radius vom Zentrum des Brunnens ($r$), der Referenzhöhe der Wassersäule ($h_0$) und dem Radius des Brunnens ($r_0$) am Rand des Brunnens sowie der charakteristischen Fließlänge im Boden ($s_0$) berechnet wird, hat folgende Form:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \displaystyle\frac{ 2 r_0 }{ s_0 }\ln\left(\displaystyle\frac{ r }{ r_0 }\right)} $ |
Diese Lösung wird grafisch in Abhängigkeit von den zusätzlichen Faktoren $h/h_0$ und $r/r_0$ für verschiedene $r_0/s_0$ wie folgt dargestellt:
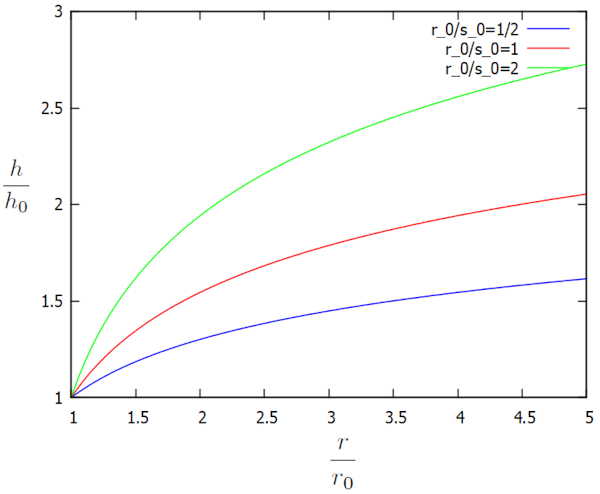
Das Profil zeigt, dass die Höhe der Wassersäule weit vom Brunnen entfernt bemerkenswert hoch ist. Aufgrund der Wasserentnahme durch den Brunnen beginnt diese Höhe jedoch zu sinken, bis sie den Rand des Brunnens erreicht. Dynamisch bestimmt die Flussdichte ($j_s$) die Menge des zum Brunnen fließenden Wassers, während sich die Referenzhöhe der Wassersäule ($h_0$) allmählich anpasst, bis ein Gleichgewichtszustand erreicht ist. Mit anderen Worten: Ist der Wert der Referenzhöhe der Wassersäule ($h_0$) im Verhältnis zur gesamten Wassermenge, die den Brunnen erreicht, zu niedrig, steigt er an; ist er zu hoch, sinkt er. Somit nimmt die Referenzhöhe der Wassersäule ($h_0$) den Wert an, der die Menge des ankommenden Wassers mit der Menge des durch den Brunnen entnommenen Wassers ausgleicht.
ID:(883, 0)
Flussdichtelösung in Richtung eines Brunnens
Gleichung 
Die Lösung, die für die Höhe und die Flussparameter an einem Referenzpunkt ($j_{s0}$) sowie den Radius vom Zentrum des Brunnens ($r$), den Radius des Brunnens ($r_0$) und die charakteristische Fließlänge im Boden ($s_0$) erhalten wurde, zeigt, dass die Flussdichte ($j_s$) gleich ist:
| $ \displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{1}{\displaystyle\frac{ r }{ r_0 }\sqrt{1 + \displaystyle\frac{ 2 r_0 }{ s_0 }\ln\left(\displaystyle\frac{r}{r_0}\right)}}$ |
Diese Lösung wird grafisch in Abhängigkeit von den zusätzlichen Faktoren $j_s/j_{s0}$ und $r/r_0$ für verschiedene $r_0/s_0$ wie folgt dargestellt:
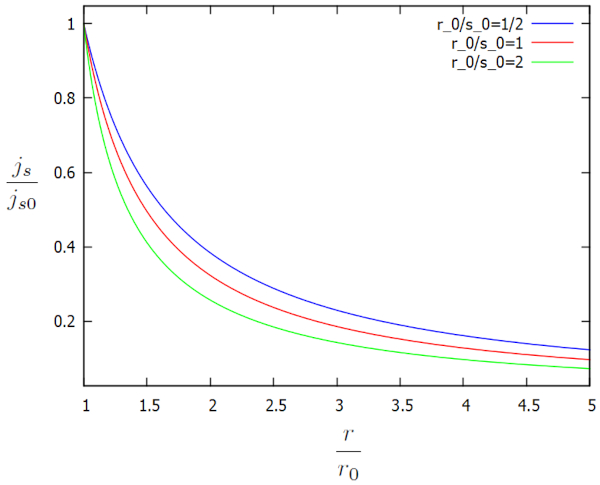
Die Flussdichte ($j_s$) nimmt weiter zu, je näher wir dem Kanal kommen, während die Höhe der Wassersäule im Boden ($h$) abnimmt. Diese Zunahme ist notwendig, um die Fließgeschwindigkeit in der Flussdichte ($j_s$) aufrechtzuerhalten oder zu erhöhen.
ID:(884, 0)
Strömungsdichte und Druckgradient
Gleichung 
Die Flussdichte ($j_s$) kann als Funktion der Höhe der Wassersäule im Boden ($h$) oder in Bezug auf den Druck der Wassersäule ($p$), der durch die Flüssigkeitssäule erzeugt wird, ausgedrückt werden. Unter Verwendung der Definition der Bodenpermeabilität ($k_s$) ergibt sich die folgende Beziehung für die Viskosität ($\eta$) und die Position der Wassersäule im Boden ($x$):
| $ j_s = -\displaystyle\frac{ k_s }{ \eta }\displaystyle\frac{ dp }{ dx }$ |
ID:(885, 0)
Bodendurchlässigkeit
Gleichung 
Die Bodenpermeabilität ($k_s$) steht in Beziehung zum Radius eines generischen Korns ($r_0$), zur Porosität ($f$) und zur spezifischen generischen Porosität ($q_0$) durch die folgende Gleichung:
| $ k_s \equiv \displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}$ |
ID:(886, 0)
