Pozo de agua
Storyboard 
Las fuentes de agua corresponden a vertientes superficiales y pozos perforados. En el caso de las vertientes superficiales, el agua puede fluir directamente a un estanque desde donde se distribuye. En el caso de los pozos perforados, es necesario extraer el agua mediante una bomba que luego la vierte en el estanque para su posterior distribución.
ID:(144, 0)
Flujo hacia un pozo
Ecuación 
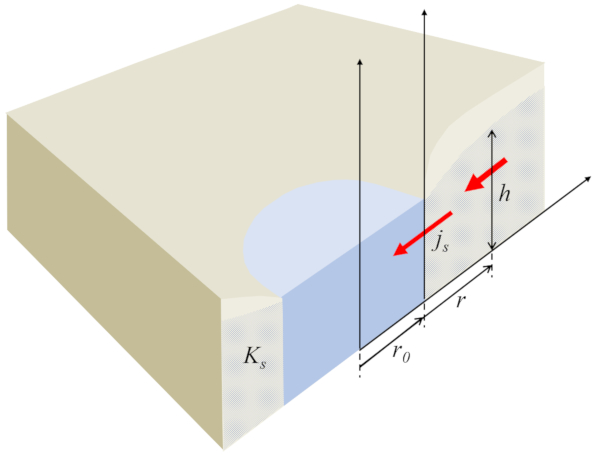
Podemos analizar el caso estacionario, lo cual significa que la relación entre la altura de la columna de agua en el suelo ($h$) y la densidad de flujo ($j_s$) debe permanecer constante. En particular, esto puede evaluarse en un punto específico, utilizando la altura de referencia de la columna de agua ($h_0$) y el flujo en dicho punto de referencia ($j_{s0}$):
| $ h j_s = h_0 j_{s0} $ |
que define el perfil del agua en el suelo:
ID:(882, 0)
Solución altura del flujo hacia un pozo
Ecuación 
La solución de la ecuación de flujo en una dimensión hacia un pozo, en la cual se calcula el valor de la altura de la columna de agua en el suelo ($h$) en función del radio desde el centro del pozo ($r$), la altura de referencia de la columna de agua ($h_0$), y el radio del pozo de agua ($r_0$) en el borde del pozo, junto con el largo característico del flujo en el suelo ($s_0$), tiene la siguiente forma:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \displaystyle\frac{ 2 r_0 }{ s_0 }\ln\left(\displaystyle\frac{ r }{ r_0 }\right)} $ |
Esta solución se representa gráficamente en función de los factores adicionales $h/h_0$ y $r/r_0$ para distintos $r_0/s_0$ de la siguiente manera:
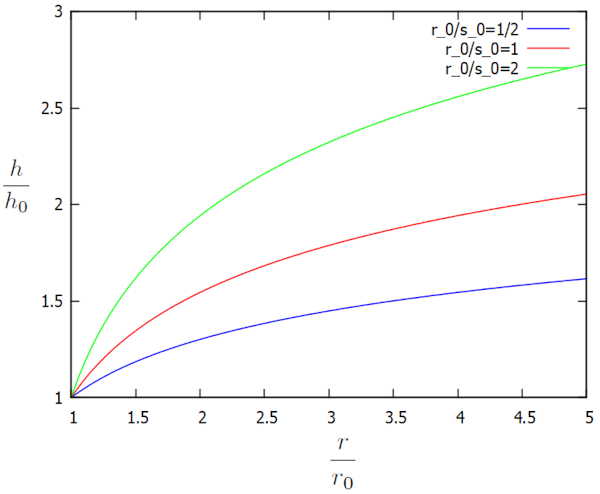
El perfil revela que, lejos del pozo, la altura de la columna de agua es notablemente alta. Sin embargo, debido a la extracción de agua por el pozo, esta altura comienza a disminuir hasta alcanzar el borde del pozo. De manera dinámica, la densidad de flujo ($j_s$) determina la cantidad de agua que fluye hacia el pozo, mientras que la altura de referencia de la columna de agua ($h_0$) se ajusta gradualmente hasta alcanzar un estado de equilibrio. En otras palabras, si el valor de la altura de referencia de la columna de agua ($h_0$) es demasiado bajo en relación con la cantidad total de agua que llega al pozo, se incrementa; y si es demasiado alto, disminuye. Así, la altura de referencia de la columna de agua ($h_0$) adquiere el valor que equilibra la cantidad de agua que llega con la cantidad de agua que se extrae a través del pozo.
ID:(883, 0)
Solución densidad de flujo hacia un pozo
Ecuación 
La solución obtenida para la altura y los parámetros del flujo en un punto de referencia ($j_{s0}$) y el radio desde el centro del pozo ($r$), el radio del pozo de agua ($r_0$) y el largo característico del flujo en el suelo ($s_0$) nos muestra que la densidad de flujo ($j_s$) es igual a:
| $ \displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{1}{\displaystyle\frac{ r }{ r_0 }\sqrt{1 + \displaystyle\frac{ 2 r_0 }{ s_0 }\ln\left(\displaystyle\frac{r}{r_0}\right)}}$ |
Esta solución se representa gráficamente en función de los factores adicionales $j_s/j_{s0}$ y $r/r_0$ para distintos $r_0/s_0$ de la siguiente manera:
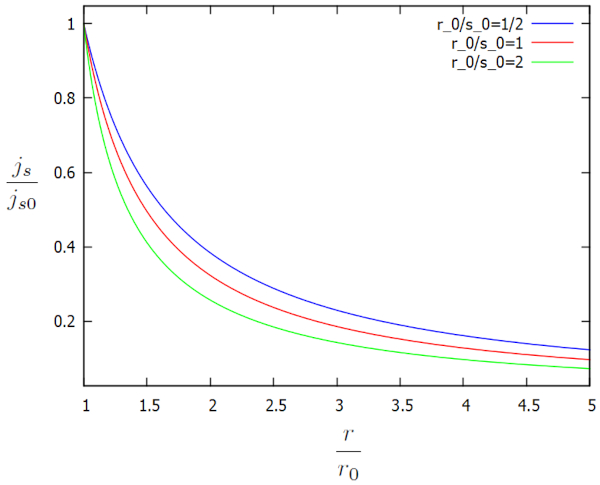
La densidad de flujo ($j_s$) continúa aumentando a medida que nos acercamos al canal, mientras que la altura de la columna de agua en el suelo ($h$) disminuye. Este aumento es necesario para mantener la velocidad del flujo en la densidad de flujo ($j_s$) o, en su defecto, para incrementarla.
ID:(884, 0)
Densidad de flujo y gradiente de presión
Ecuación 
La densidad de flujo ($j_s$) se puede expresar en función de la altura de la columna de agua en el suelo ($h$) o de la presión de la columna de agua ($p$) generada por la columna de líquido. Empleando la definición de la permeabilidad del suelo ($k_s$), se obtiene la siguiente relación para la viscosidad ($\eta$) y la posición de la columna de agua en el suelo ($x$):
| $ j_s = -\displaystyle\frac{ k_s }{ \eta }\displaystyle\frac{ dp }{ dx }$ |
ID:(885, 0)
Permeabilidad del suelo
Ecuación 
La permeabilidad del suelo ($k_s$) se relaciona con el radio de un grano genérico ($r_0$), la porosidad ($f$) y la porosidad específica genérica ($q_0$) a través de la siguiente fórmula:
| $ k_s \equiv \displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}$ |
ID:(886, 0)
