Water well
Storyboard 
Water sources include surface springs and drilled wells. In the case of surface springs, the water can flow directly into a tank for distribution. For drilled wells, it is necessary to extract the water using a pump, which then delivers the water to the tank for further distribution.
ID:(144, 0)
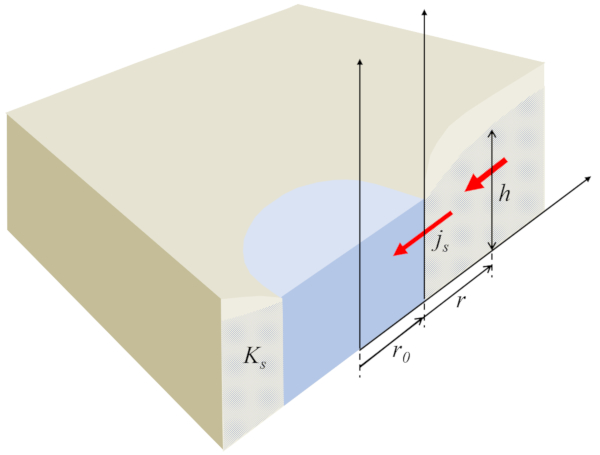
Flow into a well
Equation 
We can analyze the steady-state case, which implies that the height of the water column in the soil ($h$) divided by the flux density ($j_s$) must remain constant and, specifically, can take values at a specific point represented by the reference height of the water column ($h_0$) and the flux at a reference point ($j_{s0}$):
| $ h j_s = h_0 j_{s0} $ |
which defines the water profile in the ground:
ID:(882, 0)
Flow height solution towards a well
Equation 
The solution to the one-dimensional flow equation towards a well, where the height of the water column in the soil ($h$) is calculated as a function of the radius from the center of the well ($r$), the reference height of the water column ($h_0$), and the radius of the well ($r_0$) at the well's edge, along with the characteristic length of the flow in the soil ($s_0$), has the following form:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \displaystyle\frac{ 2 r_0 }{ s_0 }\ln\left(\displaystyle\frac{ r }{ r_0 }\right)} $ |
This solution is graphically represented in terms of the additional factors $h/h_0$ and $r/r_0$ for different $r_0/s_0$ as follows:
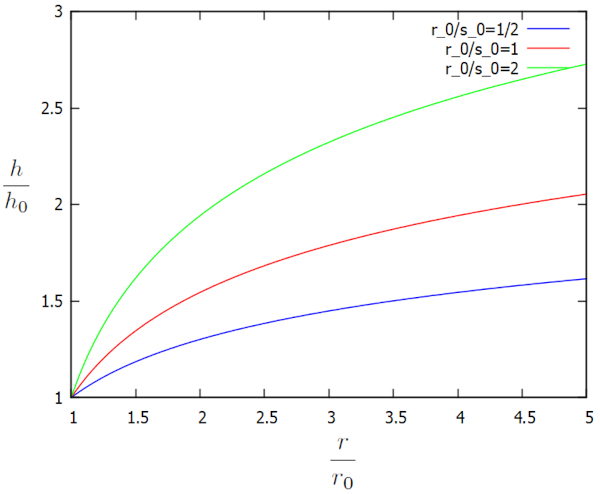
The profile reveals that, far from the well, the height of the water column is notably high. However, due to the water extraction by the well, this height begins to decrease until it reaches the well's edge. Dynamically, the flux density ($j_s$) determines the amount of water flowing towards the well, while the reference height of the water column ($h_0$) adjusts gradually until reaching an equilibrium state. In other words, if the value of the reference height of the water column ($h_0$) is too low relative to the total amount of water reaching the well, it increases; and if it is too high, it decreases. Thus, the reference height of the water column ($h_0$) acquires the value that balances the amount of water arriving with the amount of water extracted through the well.
ID:(883, 0)
Flux density solution towards a well
Equation 
The solution obtained for the height and flow parameters at a reference point ($j_{s0}$) and the radius from the center of the well ($r$), the radius of the well ($r_0$), and the characteristic length of flow in the soil ($s_0$) shows that the flux density ($j_s$) is equal to:
| $ \displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{1}{\displaystyle\frac{ r }{ r_0 }\sqrt{1 + \displaystyle\frac{ 2 r_0 }{ s_0 }\ln\left(\displaystyle\frac{r}{r_0}\right)}}$ |
This solution is graphically represented in terms of the additional factors $j_s/j_{s0}$ and $r/r_0$ for different $r_0/s_0$ as follows:
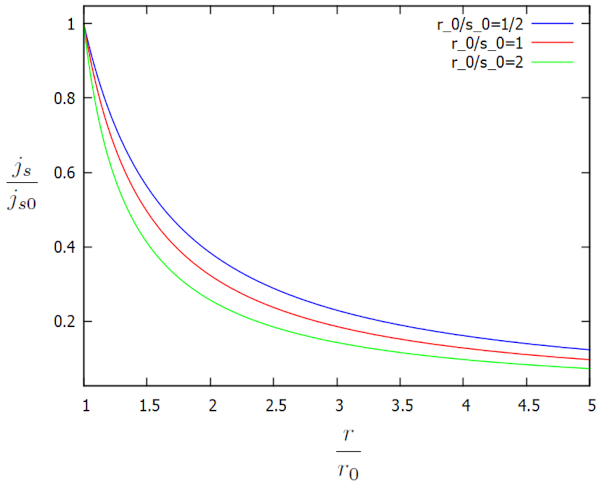
The flux density ($j_s$) continues to increase as we approach the channel, while the height of the water column in the soil ($h$) decreases. This increase is necessary to maintain or enhance the flow velocity in the flux density ($j_s$).
ID:(884, 0)
Flow density and pressure gradient
Equation 
The flux density ($j_s$) can be expressed as a function of the height of the water column in the soil ($h$) or in terms of the pressure of the water column ($p$) generated by the liquid column. Using the definition of soil permeability ($k_s$), the following relationship is obtained for the viscosity ($\eta$) and the position of the water column in the soil ($x$):
| $ j_s = -\displaystyle\frac{ k_s }{ \eta }\displaystyle\frac{ dp }{ dx }$ |
ID:(885, 0)
Soil permeability
Equation 
Soil permeability ($k_s$) is related to the radius of a generic grain ($r_0$), porosity ($f$), and generic specific porosity ($q_0$) through the following equation:
| $ k_s \equiv \displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}$ |
ID:(886, 0)
