Storyboard

A casa estará exposta ao ambiente e, por isso, deve ser projetada levando em consideração os diferentes aspectos que a afetarão, a fim de encontrar a melhor estratégia para minimizar os efeitos.

• É particularmente importante considerar os efeitos do vento e da chuva e tomar medidas para minimizar a entrada de água por portas, janelas e vazamentos.

• Além disso, deve-se levar em conta a exposição à temperatura e ao vento, pois isso afetará a resistência térmica e, consequentemente, os custos de aquecimento.

A seguir, apresentamos como obter informações climáticas históricas no site openweathermap.org e realizar uma primeira exploração dos dados para este projeto. A mesma operação pode ser realizada para qualquer outra localização, desde que os dados correspondentes sejam adquiridos.

>Modelo

ID:(64, 0)

Descrição

>Top

Para acessar o aplicativo, você tem duas opções:

1. Usando as imagens no lado direito da página principal:

• Clique no logotipo do Spyrit no canto superior esquerdo para acessar a página principal.
• Uma vez na página principal, você pode navegar pelas imagens localizadas no lado direito.
• Use as setas "<" (esquerda) e ">" (direita) para se deslocar entre as imagens.
• Quando encontrar a imagem desejada, clique nela e o aplicativo será carregado.

2. Usando o menu de navegação no lado esquerdo:

• Vá para a seção "Conhecimento" no menu de navegação, localizado no lado esquerdo.
• Em seguida, selecione "Palos Verdes" no menu suspenso.
• Depois, escolha a opção "Clima" dentro da seção Palos Verdes.
• Selecione "Caracterização" no submenu.
• Por fim, escolha "Dados climáticos chave".
• Ao seguir essas etapas, o aplicativo será carregado.

ID:(472, 0)

Descrição

>Top

Para consultar os dados baixados do openweathermap.org (veja a apresentação relacionada), primeiro você precisa selecionar o arquivo. Para isso, clique no botão "Carregar" e localize o arquivo no formato CSV:

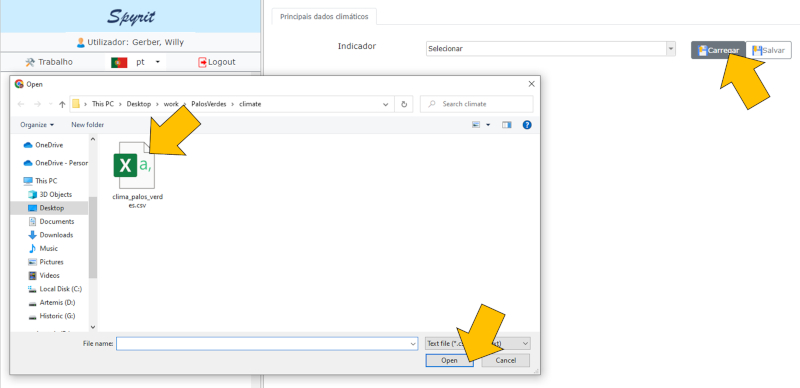
Após confirmar, os dados serão carregados e estarão disponíveis para consulta.

ID:(456, 0)

Descrição

>Top

Uma vez selecionados os dados para visualização, eles são apresentados tanto em forma gráfica, indicando o valor médio, o valor médio mais e menos o desvio padrão, quanto em uma tabela com os valores numéricos:

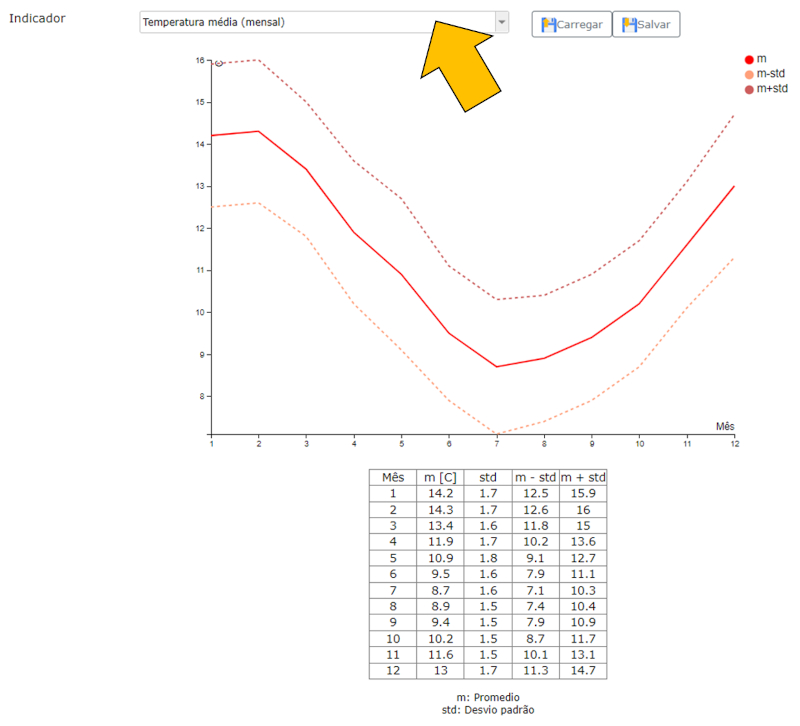
Os dados estão estruturados da seguinte forma:

• Médias anuais de todos os meses.

• Médias mensais de todos os anos.

A representação gráfica nos permite visualizar possíveis tendências de mudanças mais sistemáticas, como mudanças climáticas ou variações ambientais. A análise mensal nos oferece uma visão de como o parâmetro varia ao longo do ano.

ID:(457, 0)

Descrição

>Top

Uma vez selecionados os dados para visualização, eles são apresentados tanto graficamente, exibindo o valor médio, o valor médio acrescido do desvio padrão na parte superior e o valor médio subtraído do desvio padrão na parte inferior, quanto em uma tabela com os valores numéricos:

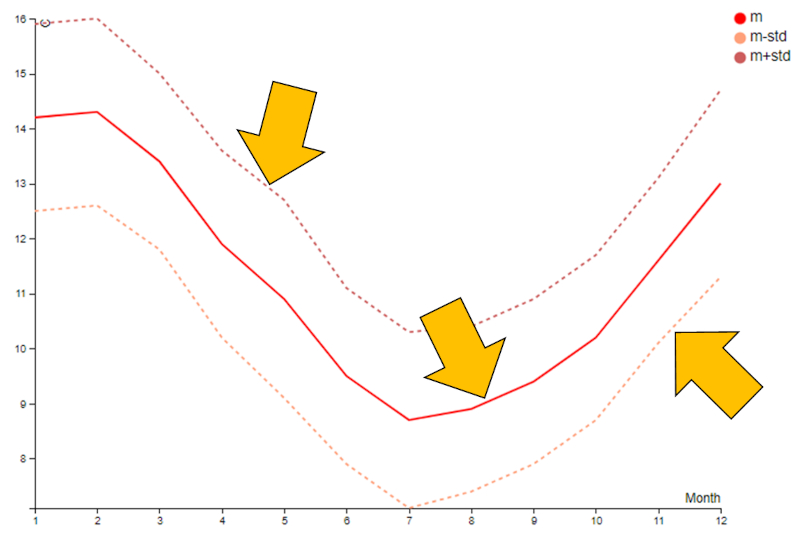
Os dados estão estruturados da seguinte forma:

• Médias anuais de todos os meses.
• Médias mensais de todos os anos.

A equação para calcular a média é:

$\bar{x}=\displaystyle\frac{1}{N}\displaystyle\sum_{i=1}^N x_i$

Onde $x_i$ representa o valor $i$-ésimo e $N$ é o número de valores.

Além disso, é calculado o desvio padrão para fornecer uma compreensão da variabilidade presente no valor médio, ou seja, o quanto ele pode variar. O desvio padrão $\sigma$ é calculado usando a seguinte equação:

$\sigma^2=\displaystyle\frac{1}{N}\displaystyle\sum_{i=1}^N x_i^2 - \bar{x}^2$

No caso de uma distribuição gaussiana dos dados, é válido que 34,1% dos dados estejam entre os valores $\bar{x}-\sigma$ e o valor médio $\bar{x}$, e de forma semelhante, 34,1% estejam entre o valor médio $\bar{x}$ e $\bar{x}+\sigma$. Isso significa que, neste caso, 68,2% dos dados estão dentro da faixa de $\bar{x}-\sigma$ a $\bar{x}+\sigma$:

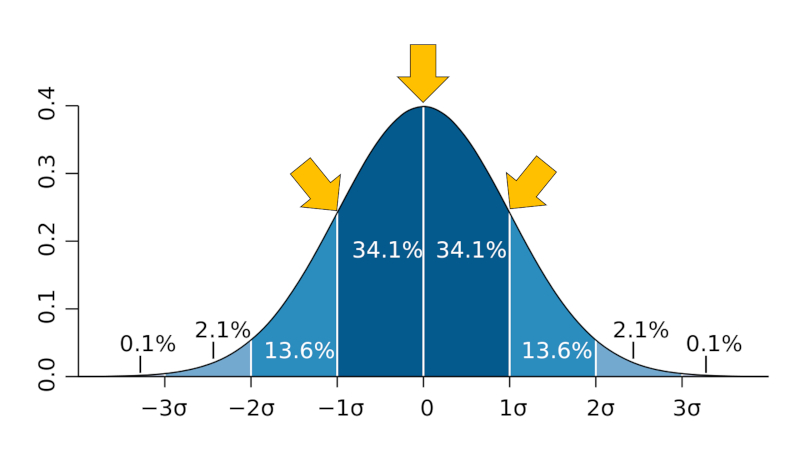
É importante observar que:

A distribuição não é necessariamente gaussiana.

Se a distribuição não for gaussiana, a faixa $[\bar{x}-\sigma,\bar{x}+\sigma]$ pode conter valores que não fazem sentido. Por exemplo, pode haver valores negativos ou valores maiores que 100% quando a faixa deveria estar dentro de $[0,100]$.

Portanto, o desvio padrão deve ser interpretado como uma medida da dispersão dos valores, ou seja, o quão provável é que eles sejam encontrados em torno do valor médio.

ID:(473, 0)

Descrição

>Top

A média anual exibe um valor médio 11.3°C que varia mínimamente, sem mostrar nenhuma tendência anômala:

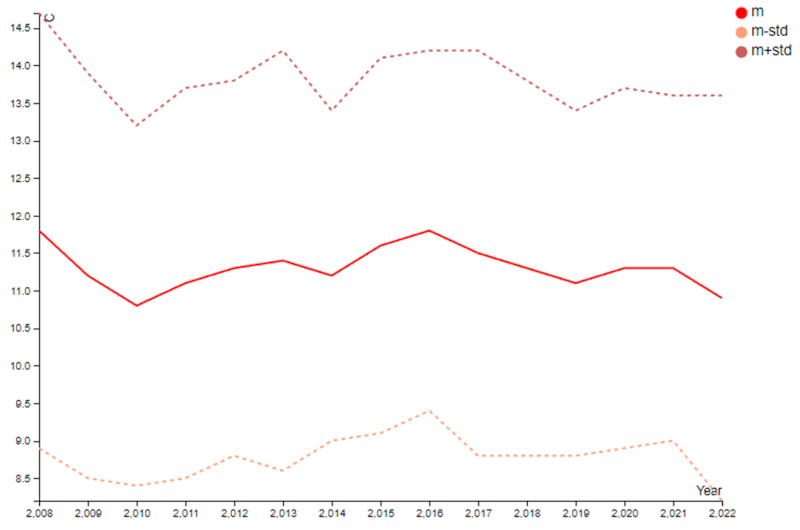
Da mesma forma, o desvio padrão mantém-se constante, não apresentando nenhuma tendência de variação nas flutuações.

ID:(458, 0)

Descrição

>Top

A média mensal mostra claramente o perfil de uma localização no hemisfério sul, com um pico no verão em torno de 14,3°C em fevereiro e um mínimo em torno de 8,7°C em julho:

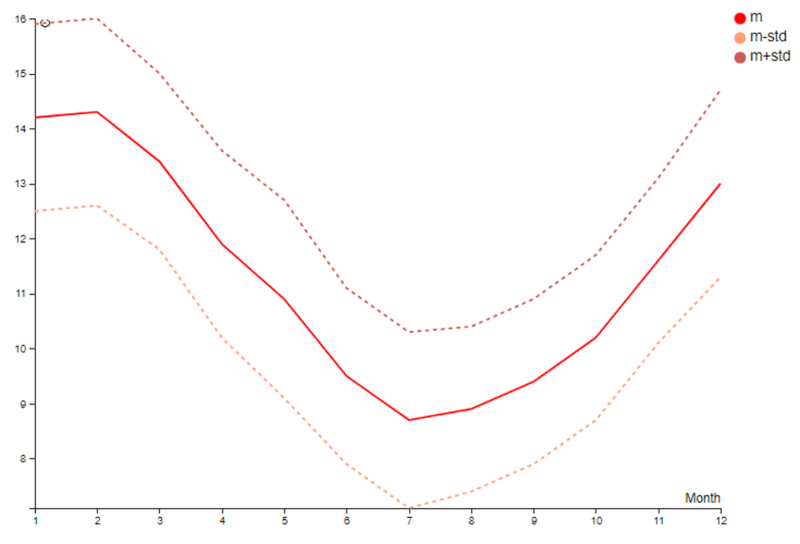
No entanto, é importante notar que o desvio padrão não é insignificante, o que significa que um mês de julho individual pode ter uma temperatura média significativamente mais baixa (por exemplo, 7°C) ou mais alta (por exemplo, 10°C). Isso indica que pode haver variações significativas de temperatura dentro do mesmo mês.

ID:(459, 0)

Descrição

>Top

A velocidade média do vento tem se mantido em torno de 5,9 m/s ao longo dos anos, sem mostrar nenhuma tendência anômala:

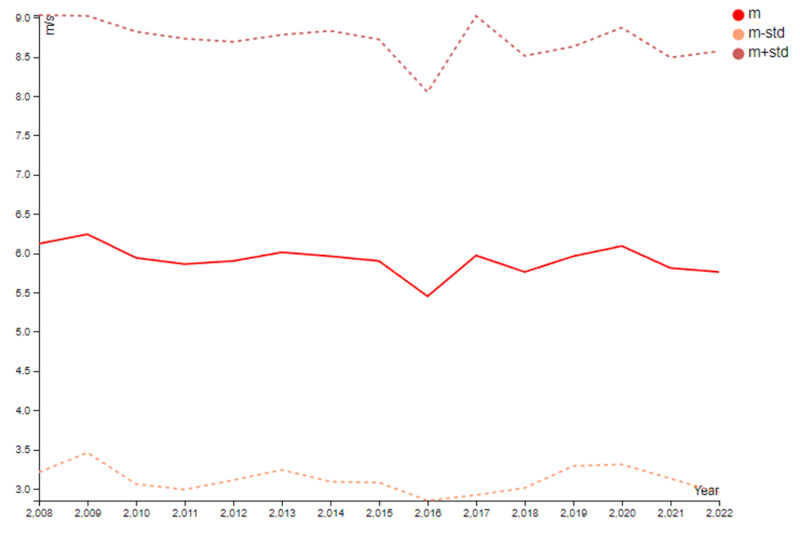
Da mesma forma, o desvio padrão permanece constante, não mostrando nenhuma tendência a variar nas flutuações.

O valor pode ser considerado alto e é diretamente influenciado pelo fato de a localização estar na costa.

ID:(460, 0)

Descrição

>Top

Na tabela de médias mensais, é possível observar que a velocidade do vento apresenta uma leve diminuição no outono e um aumento no inverno:

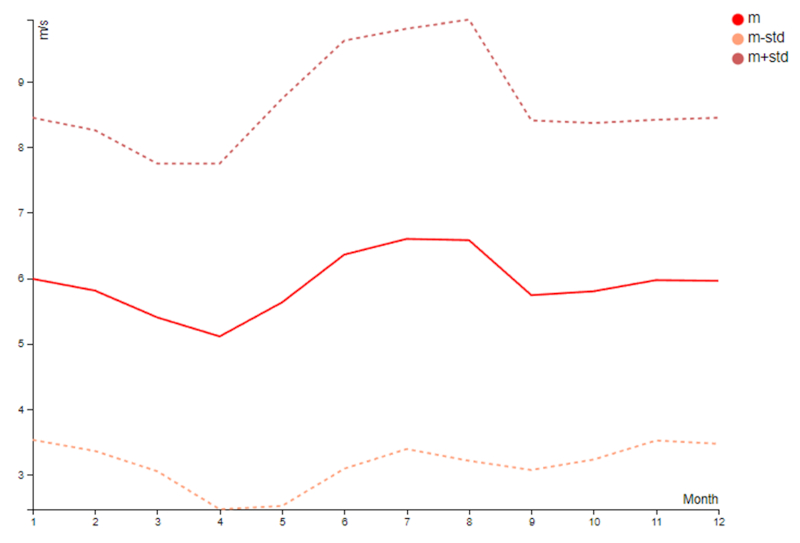
No entanto, essa variação é relativamente pequena em comparação com o desvio padrão.

ID:(461, 0)

Descrição

>Top

La precipitação pluviométrica por hora está na ordem de 0.96 mm/h e tem se mantido ao longo dos anos, sem mostrar nenhuma tendência anômala:

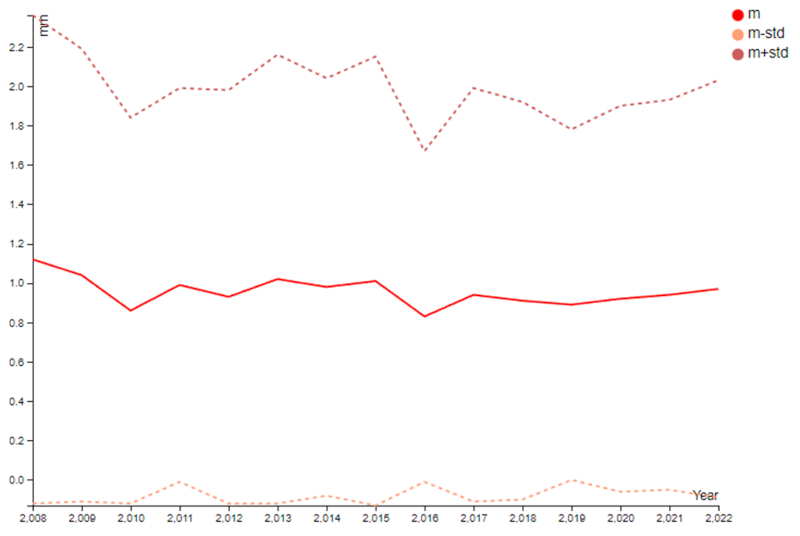
Da mesma forma, o desvio padrão se mantém constante, sem mostrar nenhuma tendência a variar nas flutuações.

Neste caso, a curva mais baixa alcança valores negativos, o que não faz sentido. Isso reflete que a distribuição não segue uma forma gaussiana e, portanto, o desvio padrão não necessariamente representa a largura de uma curva em formato de sino, como discutido anteriormente.

ID:(462, 0)

Descrição

>Top

Na tabela de médias mensais, observa-se que a quantidade de chuva por hora apresenta um leve aumento no inverno:



No entanto, essa variação é relativamente pequena em comparação com o desvio padrão.

Neste caso, a curva mais baixa alcança valores negativos, o que não faz sentido. Isso reflete que a distribuição não segue uma forma gaussiana e, portanto, o desvio padrão não necessariamente representa a largura de uma curva em formato de sino, como discutido anteriormente.

ID:(463, 0)

Descrição

>Top

A fração do tempo em que chove tem se mantido em torno de 24,8% ao longo dos anos, sem mostrar nenhuma tendência anômala:

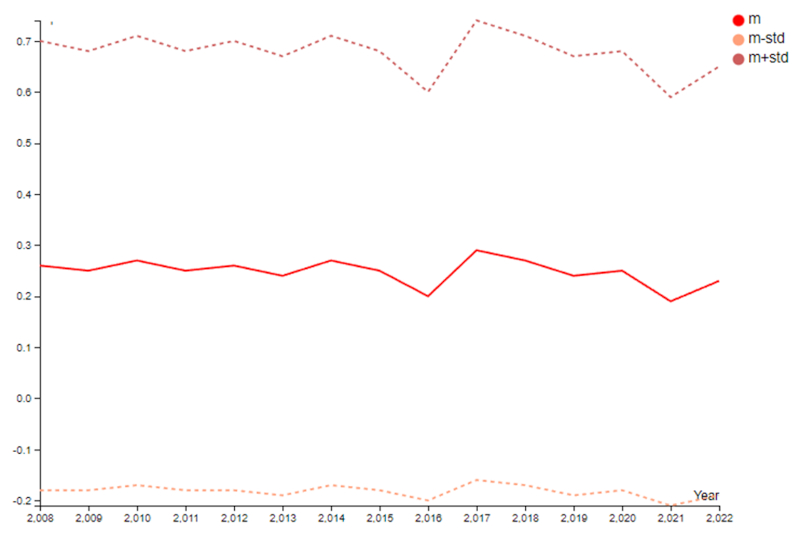
Da mesma forma, o desvio padrão permanece constante, sem mostrar nenhuma tendência a variar nas flutuações.

Neste caso, a curva mais baixa alcança valores negativos, o que não faz sentido. Isso reflete que a distribuição não segue uma forma gaussiana e, portanto, o desvio padrão não necessariamente representa a largura de uma curva em formato de sino, como discutido anteriormente.

ID:(464, 0)

Descrição

>Top

Na tabela de médias mensais, observa-se que a fração de tempo em que chove é menor no verão, em torno de 10%, e aumenta no inverno, chegando a aproximadamente 44%:

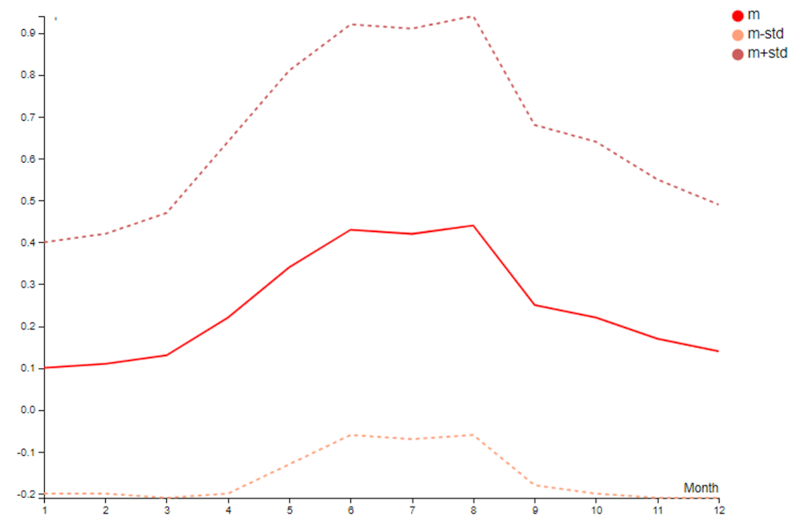
A variação entre verão e inverno é da mesma ordem de grandeza do desvio padrão, indicando uma mudança significativa que vai além da faixa de flutuações normais.

Neste caso, a curva mais baixa alcança valores negativos, o que não faz sentido. Isso reflete que a distribuição não segue uma forma gaussiana e, portanto, o desvio padrão não necessariamente representa a largura de uma curva em formato de sino, como discutido anteriormente.

ID:(465, 0)

Descrição

>Top

A cobertura de nuvens manteve-se em torno de 51,9% do tempo ao longo dos anos, sem mostrar nenhuma tendência anômala:

Da mesma forma, o desvio padrão permanece constante, sem mostrar nenhuma tendência a variar nas flutuações.

ID:(466, 0)

Descrição

>Top

Na tabela de médias mensais, observa-se que a cobertura de nuvens é menor no verão, em torno de 33%, e maior no inverno, aproximadamente 67,7%:

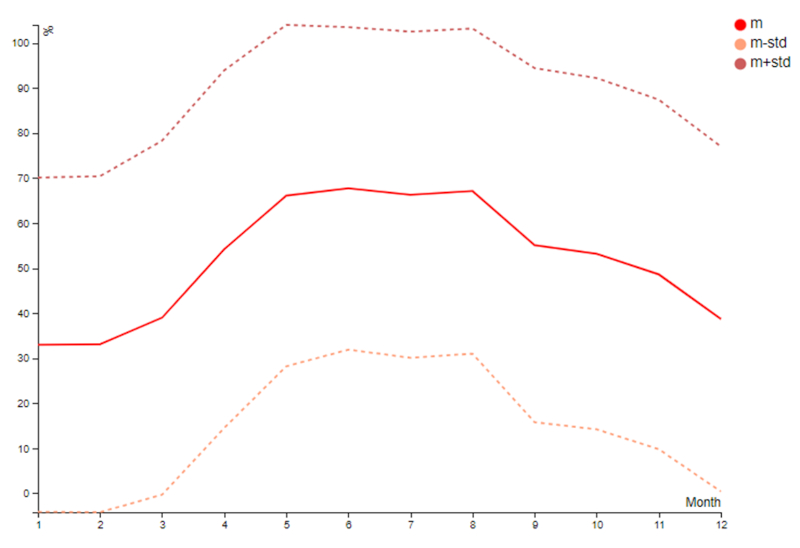
No entanto, essa variação é relativamente pequena em comparação com o desvio padrão.

Neste caso, a curva mais baixa alcança valores negativos, o que não faz sentido. Isso reflete que a distribuição não segue uma forma gaussiana e, portanto, o desvio padrão não necessariamente representa a largura de uma curva em formato de sino, como discutido anteriormente.

ID:(467, 0)

Descrição

>Top

A umidade média tem se mantido em torno de 83,9% ao longo dos anos, sem mostrar nenhuma tendência anômala:

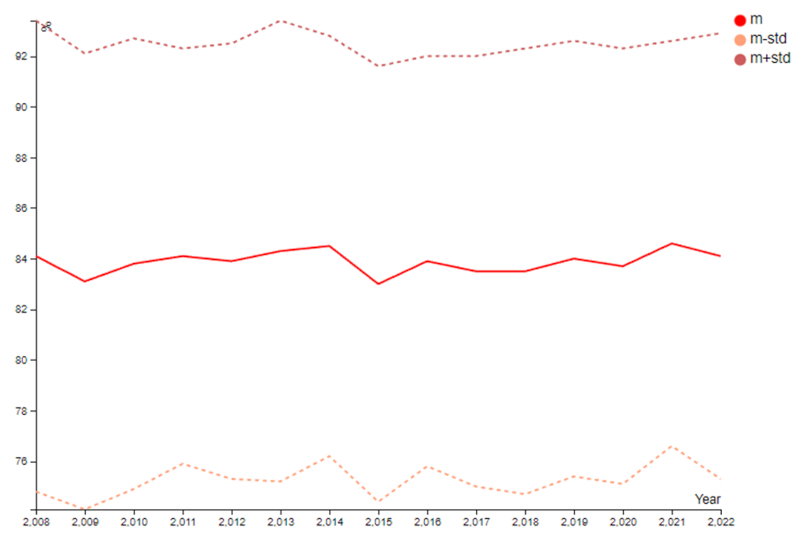
Da mesma forma, o desvio padrão permanece constante, sem mostrar nenhuma tendência a variar nas flutuações.

ID:(468, 0)

Descrição

>Top

Na tabela de médias mensais, observa-se que a umidade média apresenta apenas pequenas flutuações em torno da média anual de 83,9%:

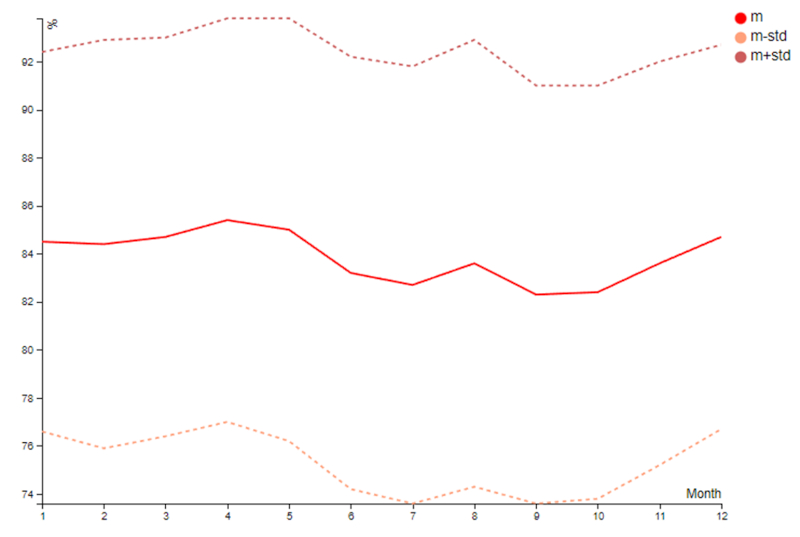
Isso provavelmente é devido à proximidade com o oceano, que, combinada com uma temperatura relativamente estável, mantém uma umidade constantemente alta ao longo do ano.

ID:(469, 0)

Descrição

>Top

No caso da média anual da pressão atmosférica, pode-se observar uma leve tendência de alta (de 1017 para 1018 bar), embora essa tendência seja muito menor do que o desvio padrão, portanto, pode não ser necessariamente significativa:

ID:(470, 0)

Descrição

>Top

Na tabela de médias mensais, observa-se que a pressão atmosférica é menor no verão e tende a aumentar até a primavera, após o que volta a diminuir:

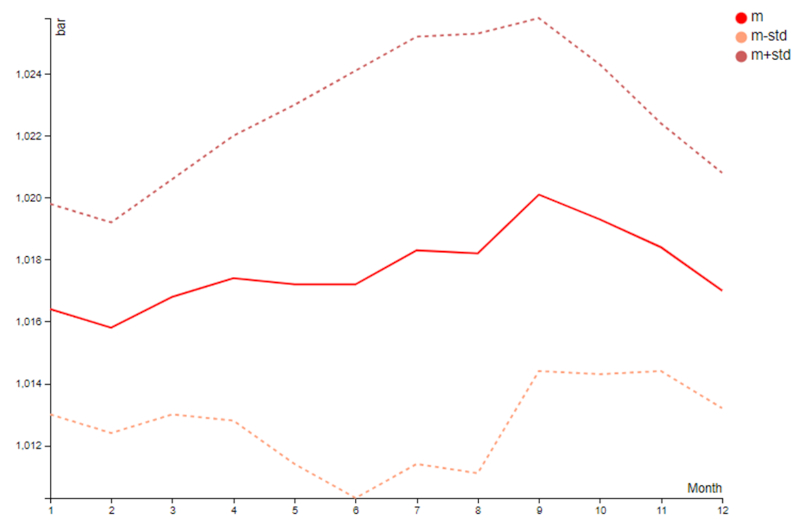
O aumento entre o verão e a primavera é da mesma ordem de grandeza que o desvio padrão do verão, indicando um efeito significativo.

ID:(471, 0)