How this website contributes
Storyboard 
The key to successfully communicating complex topics to people without advanced academic preparation is to simplify the concepts without losing their practical applicability. At the heart of this task lies the challenge of complex mathematics, which encompasses both concepts that can be relatively easily explained and algorithms that require advanced knowledge for interpretation and use.
One approach to tackle this challenge is to provide basic explanations of the algorithms and use computer tools to apply them in a practical manner. An analogy could be drawn to a modern airplane, which is highly complex, but a pilot can operate it by understanding its various functionalities without necessarily comprehending the inner workings in detail. In this sense, we focus on understanding concepts and variables, provide straightforward explanations of the algorithms used to calculate these variables, and then employ tools that apply these algorithms to the user without requiring a detailed understanding of how they work, while still ensuring an understanding of their purpose and limitations in their application.
ID:(103, 0)
Paradigm break that this web page seeks
Description 
We live in a complex world, facing a series of situations for which science allows us to understand what's happening and how we can protect ourselves or control the situation to the best of our ability. Current examples include issues like pandemics, climate change, and all the consequences of climate change, such as extreme weather and catastrophic events like landslides and floods. Most of these phenomena have been studied by science, and it can describe many of their mechanisms, enabling us to understand when they occur, how they develop, and how we can protect ourselves or reduce risks.
Furthermore, today's population is better educated than in the past. The majority have completed secondary education, and many have technical qualifications or even academic degrees. This means they can comprehend more complex physics, even if they don't necessarily have a strong grasp of the associated mathematics.
However, despite the improved education, many people lack relevant scientific knowledge because traditional topics that have been taught for centuries are still emphasized, even if they are not up-to-date or particularly relevant. One of the main reasons for this situation is that more advanced mathematics often create a barrier to understanding and applying complex scientific concepts. But this is changing, as modern computer tools make it possible for people to apply complex scientific knowledge without requiring an in-depth understanding of the mathematics behind it. It's similar to using a calculator to perform trigonometric calculations without fully comprehending how those values are obtained.
Therefore, this website aims to address these challenges by studying all aspects of designing, constructing, and operating a house and then developing projects focused on dissemination, using the most advanced science in the simplest possible way. An analogy is made to constructing a complex Lego model to enable users to apply complex knowledge without needing advanced mathematical skills.
ID:(717, 0)
Type of information
Description 
There are two types of information that can be generated and utilized in the study of systems one is involved in.
The first type comes from practical experience with related work. In this sense, it is personal experience that can be shared with others, but it has limitations since it is not necessarily universal. However, it is valuable because it cannot be deduced from a body of information and is often acquired by living through or observing others in similar situations. It is linked to a specific situation and is often difficult to generalize.
The second type corresponds to what is learned using the scientific method. This often involves creating a model that represents reality and allows for the definition of variables and parameters. This model is then subjected to experimental studies in which multiple alternatives can be explored. On the other hand, it is generally universal and should be replicable under the same conditions in any place and at any time in the future. Lastly, it tends to be largely objective as it is based on measurements and only includes subjective aspects when making conjectures about the causes of what is observed.
The first type is documented by describing the situations and providing guidelines on the points to consider when performing similar operations. In the second type, it is important to define the variables and parameters, as well as their measurement methods, and then develop models that describe how the system behaves. Finally, the second method must be validated to confirm its validity in the specific situation in which it is being applied. This validation can be simplified if the model has been studied by third parties who have conducted the necessary validations.
ID:(670, 0)
Validity of knowledge
Description 
The following pages aim to provide the knowledge that can support a project for designing and constructing a house. However, it's important to keep in mind that this is a limited endeavor because:
Every topic presented here is subject to ongoing study, so there will be additional knowledge and corrections to previous versions over time. What may be considered well-founded knowledge today may be questioned and needs to be refocused tomorrow.
Furthermore, there are limitations in the dissemination of new knowledge, so:
What is presented here may not necessarily be the most up-to-date version of knowledge available to date simply because it is difficult to monitor all contributions, and many times, valid knowledge may exist but has not yet been recognized.
Even if you have the most up-to-date and complete knowledge, its application is often limited by the precision that can be achieved. This is because:
In many cases, data is lacking, or it can only be measured with limited precision, and in others, there may be no algorithms to fully benefit from the knowledge.
Beyond the challenges of obtaining the necessary knowledge and being able to apply it, there is one last limitation stemming from the available resources:
Every study to support design and achieve successful implementation incurs costs and involves time. In this sense, perfection is the enemy of efficiency.
Therefore, it must be accepted that you will be working with incomplete and deficient knowledge and information, and decisions will have to be made based on less-than-optimal situations. However, it should not be forgotten that the studies explained here can provide guidance. The goal is not perfection but achieving the lowest possible error rate within an acceptable cost and time frame.
In summary:
The objective is to minimize errors while incurring acceptable costs and time. To achieve this, we will work with the simplest models that provide sufficiently reliable information to guide the necessary decisions for a well-designed and implemented project.
ID:(671, 0)
Common knowledge
Description 
Part of the knowledge comes from common sense and the experiences that people may have accumulated throughout their lives. Rescuing and documenting them is a way to preserve them over time and make them available to people who may not have them yet and thus provide assistance. It is highly likely that professionals may find them trivial at times and have a different experience. This does not mean that they cease to be useful for people who do not possess the knowledge.
Therefore, it is essential to keep in mind that knowledge derived from experiences can:
• Be trivial for many users.
• Contradict one's own experiences; they are not absolute in that sense.
• Have different experiences regarding the same issue that may even contradict each other; in this sense, users should interpret them and validate them according to their own criteria.
• Change over time; they are not eternal in that sense.
The most important thing is to understand that no knowledge is absolute; it represents the current state of our learning process and will inevitably change over time as more data and/or experience are gathered. The misconception that science is absolute, that what it asserts are absolute and eternal truths, and that any modification of these is a failure, shows a misunderstanding of the scientific method. The method aims to continually improve our understanding of what is happening and why. Any modification is a success because it means we have improved our knowledge, not a sign of failure of the previous understanding or the method as a whole. In that sense, any conclusion reached at a given time is the starting point for working on a new version that surpasses it, that explains what is observed more accurately and precisely. That is the scientific method.
The texts on this page include descriptive texts and notes that summarize knowledge, labeling it according to its relevance. In this sense, there are the following types of information:
An idea that may or may not be considered and only seeks to provide alternatives.
Information that may be useful for the user.
A point of attention that can be considered but does not constitute a problem in itself.
A warning that indicates a problem that may arise, for which precautions are recommended. In general, if it arises, it is possible to make corrections, which may involve time and costs.
An imminent danger that must be avoided by all means. Generally, if it cannot be avoided, more significant problems may arise, and corrections may not be easy or possible later on.
ID:(672, 0)
What does the temperature in the air mean?
Image 
The temperature of a gas is directly associated with its kinetic energy.
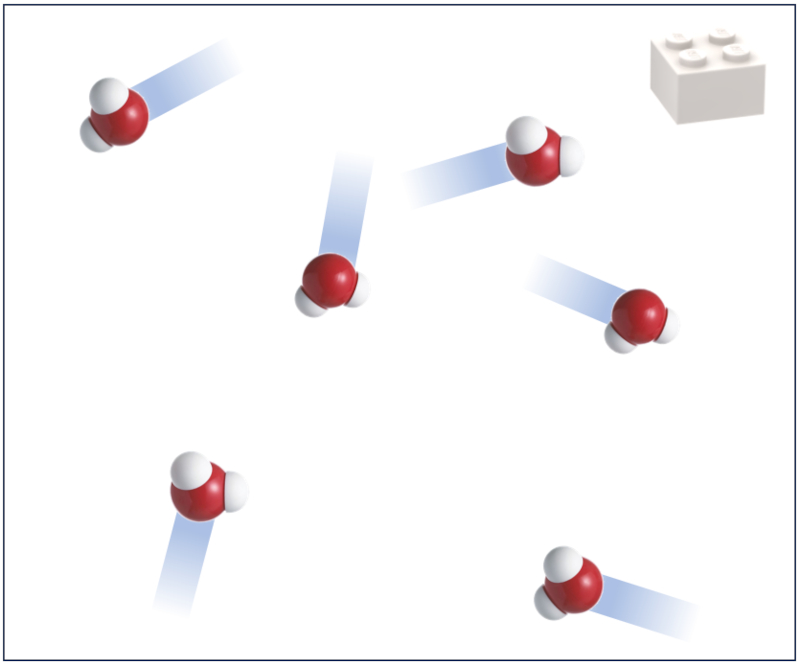
This relationship is linear but depends on constants and the degrees of freedom of the gas molecules.
Degrees of freedom refer to the number of parameters needed to describe the position and orientation of molecules. In the simplest case, a molecule can be represented with three variables for its position in space, which equates to three degrees of freedom. However, if the molecule can rotate, two additional angles are required to describe its orientation, totaling five degrees of freedom. If deformations of the molecule are also considered, additional degrees of freedom arise.
The way temperature depends on kinetic energy is important because it defines the gas's heat capacity. This means that added energy (heat) is distributed among all degrees of freedom, making it less effective in raising the temperature due to the dilution of energy.
ID:(687, 0)
What does temperature mean in a liquid or solid?
Image 
Unlike in the case of a gas, in a liquid and a solid, atoms are not free to move independently. In a crystal, for example, they occupy well-defined positions, forming a network of interacting atoms:

Ice molecules (solid)
In a liquid and amorphous materials, this ordered structure doesn't exist, but there are still forces preventing each atom from moving independently, resulting in a mass that takes the shape of its container:

Water molecules (liquid)
In both cases, the forces between atoms can be approximated as linear, similar to those of a spring. Analogously, when energy is provided, the atoms begin to oscillate, much like a mass hanging from a spring. In this way, what is kinetic energy in the case of a gas becomes energy related to oscillation in the case of a liquid and a solid. This energy is kinetic each time the atom passes through its equilibrium point, where the sum of all forces acting on it cancels out, and then it transforms into potential energy as its motion takes it away from the equilibrium point, reversing the motion to return to it.
As the famous physicist Richard Feynman once said, in the end, all processes that describe how atoms move and oscillate, which is the very essence of what we call temperature:

Richard Feynman: The world is a dynamic mess of jiggling things.
ID:(688, 0)
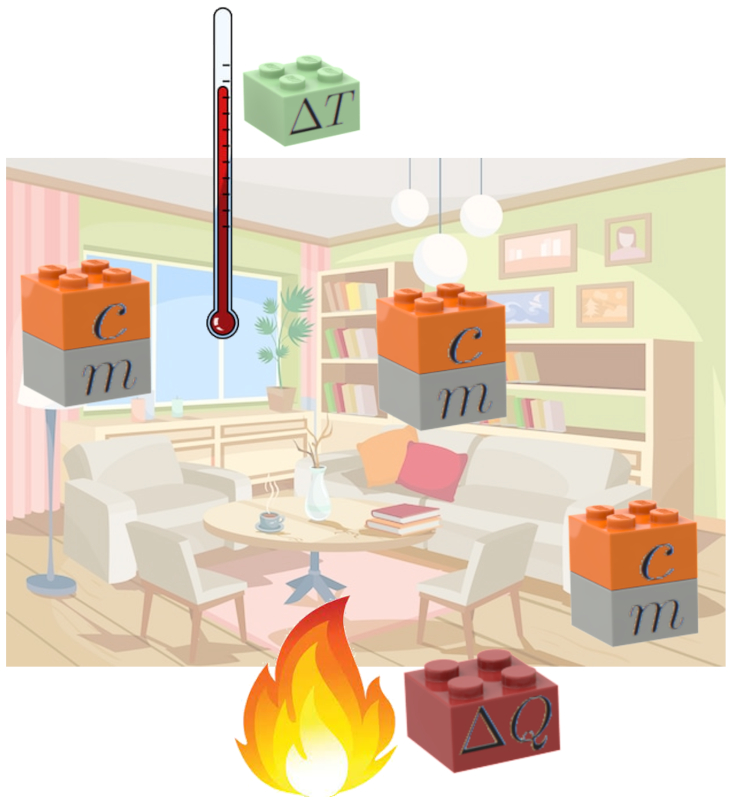
What if we want to heat a house?
Image 
Let's suppose our house is at only 12°C, and we want to heat it to 20°C. This means we need to raise the temperature of everything inside the house, including the air, by 8°C. The question is, how much heat energy, represented by a dark-colored LEGO® brick, is required to achieve this change in temperature, represented by a yellow-green LEGO® brick.

ID:(689, 0)
A little experiment
Equation 
To explore this problem, let's consider an experiment where we take a substance and heat it until we achieve the desired temperature increase.
If we conduct this experiment, we will realize that the amount of heat required depends on the amount of material we are heating, so we need to consider mass, represented here by a light gray LEGO® brick.
Additionally, we notice that the amount of heat depends on the type of substance we expose to heat. This constant, which we call the specific heat of the substance and associate with a medium orange LEGO® brick, expresses the amount of heat required to raise the temperature by one degree for one kilogram of that substance.

In this way, there is a relationship between the variables:
| Image | Meaning | Variable |
 | Temperature change | $\Delta T |
 | Mass | $m$ |
 | Specific heat | $c$ |
 | Supplied heat | $\Delta Q$ |
and a relationship between them
| Image | Meaning |
 | Heat content equation |
The mathematical relationship should reflect that the required heat $\Delta Q$ is proportional to the mass $m$ being heated and the temperature difference to be achieved $\Delta T$. The proportionality constant is called specific heat $c$ and is tabulated for various materials. Therefore, we have:
ID:(690, 0)
Identify materials to heat
Image 
To calculate the amount of heat required (represented by a dark red LEGO®) to increase the temperature (represented by a light yellow-green LEGO®), you need to identify all the materials involved, their masses (represented by a light gray LEGO®), and their respective specific heats (represented by a medium orange LEGO®):
Once you have identified and obtained the values of the masses and specific heats, you can calculate the required amount of heat directly by summing the products of the masses and specific heats multiplied by the temperature difference you want to achieve. This is represented in the following image:

ID:(691, 0)
Model utility and calculation
Description 
Calculating the heat required to raise the temperature of a house makes sense but is not necessarily the only tool we need. Firstly, in many cases, the heat equation has the issue that there are variables we cannot directly measure, such as mass in the case of air. There's no way to put all the air in a room on a scale, so we need to calculate mass using air density and room volume.
Once we've gathered all the information about masses and specific heats, we can calculate the required heat. However, this still doesn't tell us how we will generate that heat and what the cost will be. In other words, the problem is more extensive, and we must be able to estimate all the aspects that will ultimately make it useful to analyze the subject.
In summary, a series of equations or relationships are needed to explore all the relevant aspects to be useful. In our analogy, this would be akin to having many LEGO® pieces and, after clarifying what we need, assembling a fairly complex model. To design this, we could create something like an instruction manual, similar to those found in more complex LEGO® sets:

To create an instruction manual, we need to discover what type of information we may require, which data is necessary, and which can be calculated.
ID:(673, 0)
Calculation of mass from volume
Equation 
If we need to determine the mass ($m$, represented by a LEGO® brick in gray), but we only have the volume ($V$, represented by a LEGO® brick in blue), we can calculate it using the density ($\rho$, represented by a LEGO® brick in light blue):

In this case, the equation would be:
ID:(674, 0)
Calculation of temperature difference
Equation 
The relationship for calculating the required heat depends on the temperature difference, which is typically not directly measured but calculated. To do this, we need to know the current temperature ($T_1$, represented by a LEGO® brick in blue) and the desired temperature ($T_2$, represented by a LEGO® brick in red), from which we can obtain the difference ($\Delta T$, represented by a LEGO® brick in light green) by subtracting the first from the second:

This is mathematically represented as:
ID:(675, 0)
Calculation of the necessary heat
Description 
Once you have the mass ($m$, represented by a gray LEGO® brick) to be heated, the specific heat ($c$, represented by an orange LEGO® brick), and the temperature difference ($\Delta T$, represented by a light green LEGO® brick) to overcome, you can calculate the heat to be supplied ($\Delta Q$, represented by a rust-colored LEGO® brick):

In this case, the equation would be:
ID:(706, 0)
Calculation of fuel mass
Equation 
To calculate the necessary mass ($m$, represented by a LEGO® brick in gray) of the fuel, we need to know the calorific value ($C_m$, represented by an orange LEGO® brick) of the material to be used and the heat to be produced ($\Delta Q$, represented by a rust-colored LEGO® brick):

In this case, the equation would be:
At this point, it's important to note that many times, equations may reference a variable of the same type but with different meanings. In this example, we have introduced the concept of the mass to be heated, and here a second mass arises, referring to the mass of the fuel to be used. Therefore, it's crucial to keep in mind:
Different equations may refer to variables of the same type but they should be differentiated as they correspond to distinct objects (in this case, substances).
ID:(676, 0)
Fuel volume calculation
Description 
When calculating the price of fuel, it is often determined by volume rather than mass, so it is necessary to calculate the mass from the calculated fuel quantity. In this case, the density equation that was previously used is employed again, but this time it deals with the fuel instead of the material to be heated.
In this case, you have the mass of the fuel ($m$, represented by a gray LEGO® brick) and you are looking for the volume ($V$, represented by a bluish LEGO® brick), and you have the density ($\rho$, represented by a light blue LEGO® brick):

In this case, the equation would be:
| $ \rho = \displaystyle\frac{ m }{ V }$ |
At this point, it's important to note that often not only one type of variable can be used for different objects or substances. Similarly, equations can be applied in different contexts as long as they have the same physical meaning. Therefore, it's important to remember:
An equation can be employed in different contexts with different variables as long as they have the same physical meaning.
ID:(705, 0)
Calculation of cost from mass
Image 
If we need to calculate the cost ($C$, represented by a gold LEGO® brick) based on the mass ($m$, represented by a gray LEGO® brick), we can do so using the unit price ($P_m$, represented by a silver LEGO® brick):

In this case, the equation would be:
ID:(708, 0)
Calculation of cost from volume
Image 
If we need to calculate the cost ($C$, represented by a gold LEGO® brick), based on the volume ($V$, represented by a navy blue LEGO® brick), we can do so using the unit price ($P_V$, represented by a silver LEGO® brick):

In this case, the equation would be:
ID:(707, 0)
Generate the instructions
Image 
Finally, you can assemble the instructions by connecting all the steps into a large map, to which you can add a legend to remember what type of operation is being performed:

The steps include the calculation of:
1. Mass from volume.
2. The difference in temperatures between individual temperatures.
3. The required heat.
4. The mass of the fuel.
5. The volume of the fuel.
6. The cost based on mass.
7. The cost based on volume.
It's important to keep in mind that, in general, in any set of instructions:
Steps are optional and are included as needed.
Application can be done in any order, with the only requirement being that a step can only be performed if all variables except one are known.
The second point means that, for example, you can answer the question, 'How much can we heat the room if we only have X funds (costs)?' In this case, you reverse the order in which the instructions are executed, starting with the cost and ending with the final temperature.
ID:(709, 0)
The result of modeling
Image 
At the end of the modeling process, you obtain a model in the form of a map that relates ideas in the form of equations based on the model's mechanisms. The result is a network that has historically been nicknamed 'the octopus' and shares similarities with LEGO instructions:

The benefits of modeling are numerous:
Understanding how different mechanisms work and interact with each other.
The ability to anticipate the system's response when taking actions.
Enabling calculations and obtaining values that support more objective decision-making.
The name 'octopus' originated at the Universidad Austral de Chile
(UACh) in 2014 when medical students recalled the famous octopus Paul, who predicted the outcomes of the 2010 World Cup. Students began to use the graphical representation of equations as networks of equations and variables that moved like tentacles when working with them.
ID:(710, 0)
