Usuario:
Secado de la pared
Storyboard 
El secado de la pared ocurre mediante la evaporación del agua y su transporte, ya sea por difusión o por el flujo de aire. La difusión es un mecanismo muy lento, ya que se forma una zona de alta humedad sobre la superficie de la pared que dificulta la evaporación de más agua, entorpeciendo todo el proceso y prolongando dramáticamente el tiempo en que la pared permanece mojada.
Por otro lado, el flujo de aire es un mecanismo muy eficiente, ya que el agua evaporada es removida por el aire del flujo y reemplazada por aire con menor humedad, lo que puede nuevamente absorber el agua que se va evaporando.
ID:(115, 0)
Presión sobre la superficie
Concepto
El presión sobre la superficie ($p_z$), que actúa de forma vertical a la superficie:
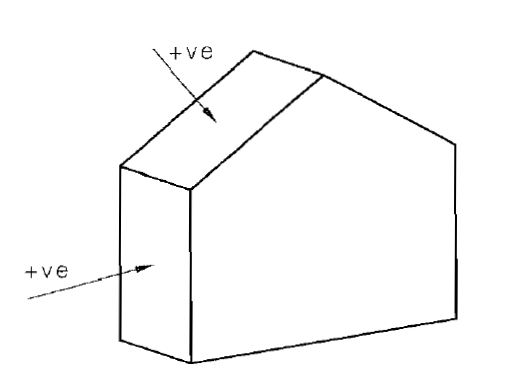
y por lo general es menor que el presión atmosférica ($p_0$) debido a los efectos del desplazamiento del aire de la densidad del aire ($\rho_a$) con la velocidad del viento con la altura ($V_z$).
En este caso, podemos modelarlo mediante la ecuación de Bernoulli con su término de energía cinética:
$\displaystyle\frac{1}{2} \rho_a V_Z^2$
Este factor se corrige con un factor que depende de la forma del cuerpo, el factor de forma aerodinámica ($C_a$), y un factor que se origina en las fluctuaciones debido a los vórtices de las turbulencias, el reducción de presión sobre la superficie ($q_z$), resultando en:
| $ q_z = \displaystyle\frac{1}{2} \rho_a V_z ^2 C_d C_a$ |
Con ello se puede calcular el presión sobre la superficie ($p_z$) resultando en:
| $ p_z = p_0 - q_z $ |
ID:(768, 0)
Factor de forma aerodinámica
Concepto
El impacto del viento en una estructura varía según la dirección en que incide sobre su superficie. Si representamos la dirección del viento con una flecha, podemos distinguir las siguientes situaciones:
| W | barlovento (contra el viento) |
| S | lateral |
| L | sotavento (con el viento) |
| U | techo inclinado contra el viento |
| R | techo inclinado con viento cruzado |
| D | techo inclinado a favor del viento |
Para comprender mejor estos conceptos, podemos consultar los ejemplos presentados en la norma AS/NZS 1170.2:
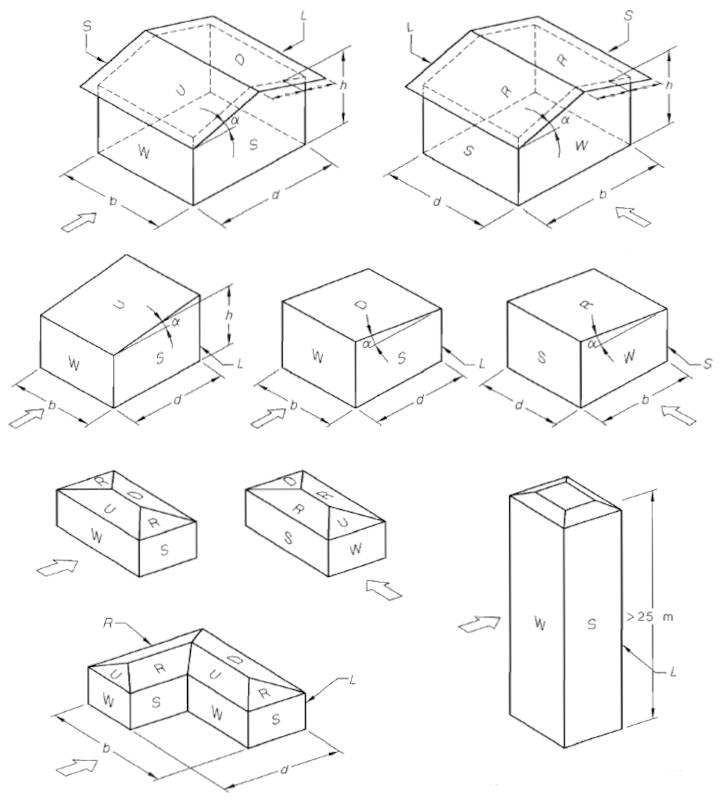
En resumen, el factor de forma aerodinámica puede modelarse como un factor que depende del ángulo entre la normal a la superficie y la dirección del viento. A partir de datos experimentales de diversas formas, este factor puede aproximarse mediante una curva de forma:
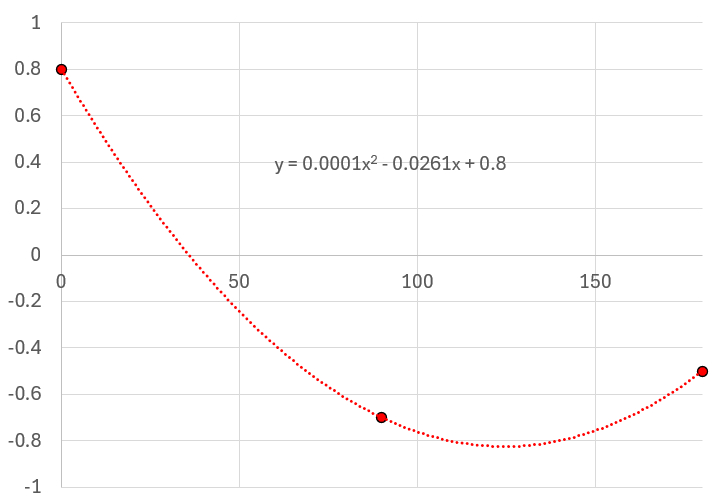
Es importante destacar que la función implica la existencia de zonas de presión positiva, pero también de zonas de presión negativa, que corresponden a áreas donde, literalmente, el viento ejerce una fuerza de succión.
ID:(760, 0)
Modelo
Concepto
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ C_a = 0.3445 \theta ^2 - 1.4961 \theta + 0.8$
C_a = 0.3445* theta ^2 - 1.4961* theta + 0.8
$ \Delta p = p_b - p_t $
Dp = p_b - p_t
$ J_V = \displaystyle\frac{ a ^3 b }{12 \eta }\displaystyle\frac{ \Delta p }{ h }$
J_V = a ^3* b * Dp /(12* eta * h)
$ p_b = p_0 - q_b $
p_z = p_0 - q_z
$ p_t = p_0 - q_t $
p_z = p_0 - q_z
$ q_b = \displaystyle\frac{1}{2} \rho_a V_b ^2 C_d C_a$
q_z = rho_a * V_z ^2* C_d * C_a /2
$ q_t = \displaystyle\frac{1}{2} \rho_a V_t ^2 C_d C_a$
q_z = rho_a * V_z ^2* C_d * C_a /2
$ V_b = \displaystyle\frac{2}{5} u \ln\left(\displaystyle\frac{ z_b }{ z_o }\right)$
V_z = 2* u * log( z / z_o )/5
$ V_t = \displaystyle\frac{2}{5} u \ln\left(\displaystyle\frac{ z_t }{ z_o }\right)$
V_z = 2* u * log( z / z_o )/5
ID:(773, 0)
Modelo de factor de forma aerodinámica
Ecuación
El factor de forma aerodinámica ($C_a$) puede ser modelado en función de el ángulo del viento ($\theta$) para estimar las contribuciones a la presión de las diferentes superficies del objeto. Este modelo se fundamenta en constantes que se derivan de mediciones realizadas en varios objetos diferentes:
| $ C_a = 0.3445 \theta ^2 - 1.4961 \theta + 0.8$ |
ID:(761, 0)
Velocidad con la altura (1)
Ecuación
La velocidad del viento con la altura ($V_z$) depende de la altura sobre el suelo ($z$). Por lo general, es prácticamente nulo en la superficie y alcanza el valor reportado en los informes meteorológicos a una altura de 10 metros. Su variación está influenciada por la rugosidad del terreno, expresada por la longitud de rugosidad ($z_o$), y por la velocidad de fricción ($u$), de la siguiente manera:
| $ V_b = \displaystyle\frac{2}{5} u \ln\left(\displaystyle\frac{ z_b }{ z_o }\right)$ |
| $ V_z = \displaystyle\frac{2}{5} u \ln\left(\displaystyle\frac{ z }{ z_o }\right)$ |
ID:(757, 1)
Velocidad con la altura (2)
Ecuación
La velocidad del viento con la altura ($V_z$) depende de la altura sobre el suelo ($z$). Por lo general, es prácticamente nulo en la superficie y alcanza el valor reportado en los informes meteorológicos a una altura de 10 metros. Su variación está influenciada por la rugosidad del terreno, expresada por la longitud de rugosidad ($z_o$), y por la velocidad de fricción ($u$), de la siguiente manera:
| $ V_t = \displaystyle\frac{2}{5} u \ln\left(\displaystyle\frac{ z_t }{ z_o }\right)$ |
| $ V_z = \displaystyle\frac{2}{5} u \ln\left(\displaystyle\frac{ z }{ z_o }\right)$ |
ID:(757, 2)
Reducción de la presión sobre la superficie (1)
Ecuación
El reducción de presión sobre la superficie ($q_z$) es la presión por unidad de área en la que se reduce sobre la superficie del cuerpo. Se modela como una modificación del modelo de Bernoulli, caracterizado por la densidad del aire ($\rho_a$) y la velocidad del viento con la altura ($V_z$), corrigiendo la dinámica con la factor de respuesta dinámica ($C_d$) y la geometría con el factor de forma aerodinámica ($C_a$):
| $ q_b = \displaystyle\frac{1}{2} \rho_a V_b ^2 C_d C_a$ |
| $ q_z = \displaystyle\frac{1}{2} \rho_a V_z ^2 C_d C_a$ |
ID:(759, 1)
Reducción de la presión sobre la superficie (2)
Ecuación
El reducción de presión sobre la superficie ($q_z$) es la presión por unidad de área en la que se reduce sobre la superficie del cuerpo. Se modela como una modificación del modelo de Bernoulli, caracterizado por la densidad del aire ($\rho_a$) y la velocidad del viento con la altura ($V_z$), corrigiendo la dinámica con la factor de respuesta dinámica ($C_d$) y la geometría con el factor de forma aerodinámica ($C_a$):
| $ q_t = \displaystyle\frac{1}{2} \rho_a V_t ^2 C_d C_a$ |
| $ q_z = \displaystyle\frac{1}{2} \rho_a V_z ^2 C_d C_a$ |
ID:(759, 2)
Presión en la superficie de un cuerpo (1)
Ecuación
El presión sobre la superficie ($p_z$) es igual a el presión atmosférica ($p_0$) reducida en el reducción de presión sobre la superficie ($q_z$):
| $ p_b = p_0 - q_b $ |
| $ p_z = p_0 - q_z $ |
ID:(776, 1)
Presión en la superficie de un cuerpo (2)
Ecuación
El presión sobre la superficie ($p_z$) es igual a el presión atmosférica ($p_0$) reducida en el reducción de presión sobre la superficie ($q_z$):
| $ p_t = p_0 - q_t $ |
| $ p_z = p_0 - q_z $ |
ID:(776, 2)
Diferencia de presión entre bordes de pared
Ecuación
La diferencia de presión entre borde inferior y superior ($\Delta p$) se calcula de la diferencia de la presión en el borde inferior ($p_b$) y la presión en el borde superior ($p_t$):
| $ \Delta p = p_b - p_t $ |
ID:(775, 0)
Flujo de vapor de agua
Ecuación
Se estima la presión en el borde superior ($p_t$) con la humedad que se desplaza por el espacio entre la pared y el revestimiento, impulsada por la diferencia de presión entre borde inferior y superior ($\Delta p$). Si asumimos que la distancia SIP y revestimiento ($a$), la distancia entre listones ($b$), la altura vertical de la pared ($h$) y la viscosidad ($\eta$):
| $ J_V = \displaystyle\frac{ a ^3 b }{12 \eta }\displaystyle\frac{ \Delta p }{ h }$ |
ID:(774, 0)