Utilizador:
Secagem de parede
Storyboard 
A secagem da parede ocorre através da evaporação da água e seu transporte, seja por difusão ou fluxo de ar. A difusão é um mecanismo muito lento, pois forma-se uma zona de alta umidade na superfície da parede, dificultando a evaporação adicional e prolongando dramaticamente o tempo em que a parede permanece molhada.
Por outro lado, o fluxo de ar é um mecanismo altamente eficiente, pois a água evaporada é removida pelo fluxo de ar e substituída por ar com menor umidade, que pode absorver mais água conforme evapora.
ID:(115, 0)
Pressão na superfície
Conceito
O pressão na superfície ($p_z$), que atua verticalmente à superfície:
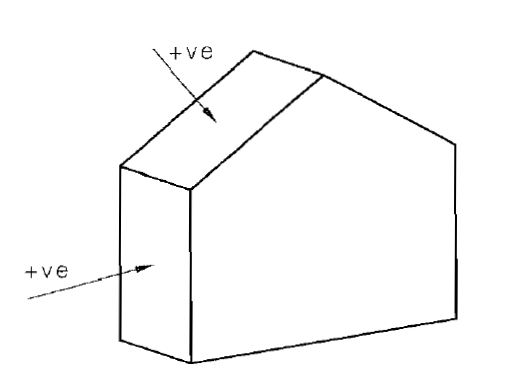
e geralmente é menor que o pressão atmosférica ($p_0$) devido aos efeitos do deslocamento do ar de la densidade do ar ($\rho_a$) com la velocidade do vento com altura ($V_z$).
Neste caso, podemos modelá-lo usando a equação de Bernoulli com seu termo de energia cinética:
$\displaystyle\frac{1}{2} \rho_a V_Z^2$
Este fator é corrigido com um fator que depende da forma do corpo, o fator de forma aerodinâmica ($C_a$), e um fator que se origina de flutuações devido a vórtices de turbulência, o redução da pressão superficial ($q_z$), resultando em:
| $ q_z = \displaystyle\frac{1}{2} \rho_a V_z ^2 C_d C_a$ |
Assim, o pressão na superfície ($p_z$) pode ser calculado resultando em:
| $ p_z = p_0 - q_z $ |
ID:(768, 0)
Fator de forma aerodinâmica
Conceito
O efeito do vento em uma estrutura depende da direção em que incide sobre a superfície. Se a direção do vento é representada por uma seta, temos as seguintes situações:
| W | a favor do vento |
| S | lateral |
| L | contra o vento |
| U | inclinação do telhado contra o vento |
| R | inclinação do telhado com vento cruzado |
| D | inclinação do telhado a favor do vento |
Para entender melhor, exemplos apresentados na norma AS/NZS 1170.2 podem ser consultados:
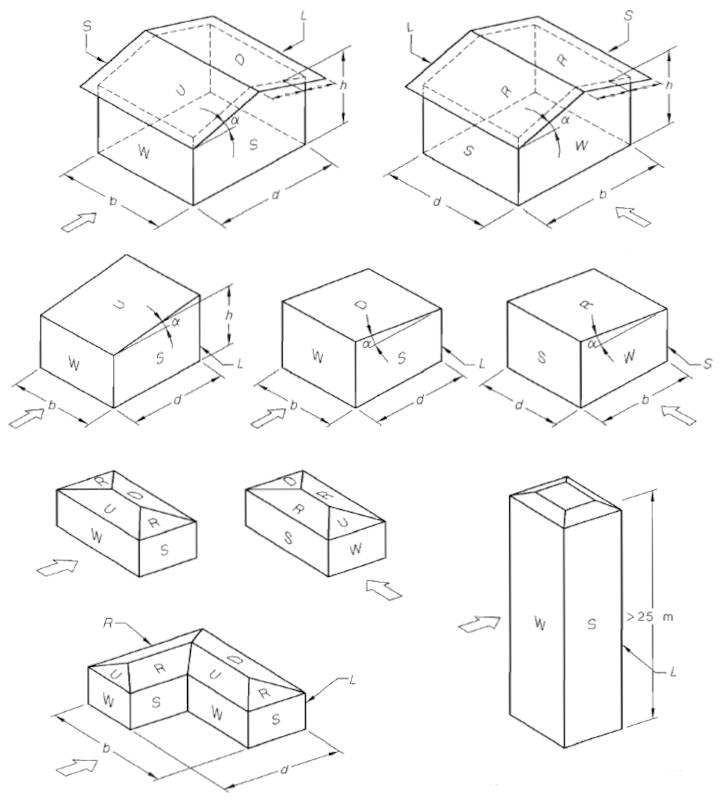
Em resumo, o fator de forma aerodinâmica pode ser modelado por um fator que depende do ângulo entre a normal à superfície e a direção do vento. Com base em dados experimentais de diversas formas, esse fator pode ser aproximado por uma curva de forma:
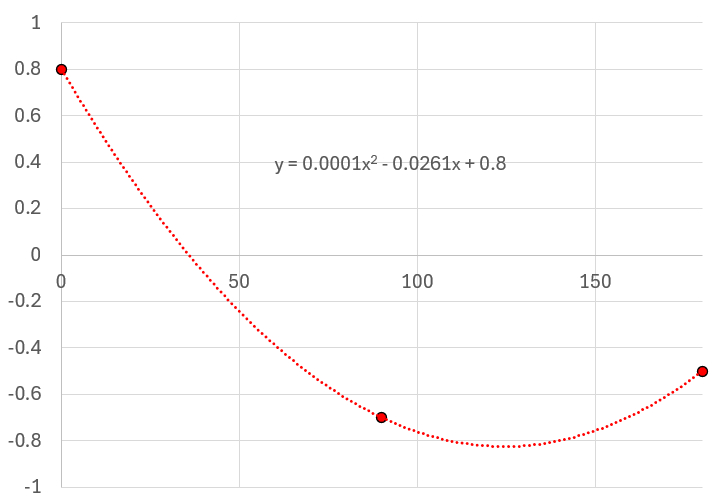
É importante perceber que a função implica a existência de zonas de pressão positiva, mas também de zonas de pressão negativa, que correspondem a áreas onde o vento literalmente suga.
ID:(760, 0)
Modelo
Conceito
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ C_a = 0.3445 \theta ^2 - 1.4961 \theta + 0.8$
C_a = 0.3445* theta ^2 - 1.4961* theta + 0.8
$ \Delta p = p_b - p_t $
Dp = p_b - p_t
$ J_V = \displaystyle\frac{ a ^3 b }{12 \eta }\displaystyle\frac{ \Delta p }{ h }$
J_V = a ^3* b * Dp /(12* eta * h)
$ p_b = p_0 - q_b $
p_z = p_0 - q_z
$ p_t = p_0 - q_t $
p_z = p_0 - q_z
$ q_b = \displaystyle\frac{1}{2} \rho_a V_b ^2 C_d C_a$
q_z = rho_a * V_z ^2* C_d * C_a /2
$ q_t = \displaystyle\frac{1}{2} \rho_a V_t ^2 C_d C_a$
q_z = rho_a * V_z ^2* C_d * C_a /2
$ V_b = \displaystyle\frac{2}{5} u \ln\left(\displaystyle\frac{ z_b }{ z_o }\right)$
V_z = 2* u * log( z / z_o )/5
$ V_t = \displaystyle\frac{2}{5} u \ln\left(\displaystyle\frac{ z_t }{ z_o }\right)$
V_z = 2* u * log( z / z_o )/5
ID:(773, 0)
Modelo de fator de forma aerodinâmico
Equação
O fator de forma aerodinâmica ($C_a$) pode ser modelado como uma função de o ângulo do vento ($\theta$) para estimar as contribuições para a pressão das diferentes superfícies do objeto. Esse modelo se baseia em constantes derivadas de medições realizadas em vários objetos diferentes:
| $ C_a = 0.3445 \theta ^2 - 1.4961 \theta + 0.8$ |
ID:(761, 0)
Velocidade com altura (1)
Equação
La velocidade do vento com altura ($V_z$) depende de la altura acima do solo ($z$). Geralmente, é praticamente nulo na superfície e alcança o valor relatado nos relatórios meteorológicos a uma altura de 10 metros. Sua variação é influenciada pela rugosidade do terreno, expressa por la comprimento de rugosidade ($z_o$), e por la velocidade de fricção ($u$), da seguinte forma:
| $ V_b = \displaystyle\frac{2}{5} u \ln\left(\displaystyle\frac{ z_b }{ z_o }\right)$ |
| $ V_z = \displaystyle\frac{2}{5} u \ln\left(\displaystyle\frac{ z }{ z_o }\right)$ |
ID:(757, 1)
Velocidade com altura (2)
Equação
La velocidade do vento com altura ($V_z$) depende de la altura acima do solo ($z$). Geralmente, é praticamente nulo na superfície e alcança o valor relatado nos relatórios meteorológicos a uma altura de 10 metros. Sua variação é influenciada pela rugosidade do terreno, expressa por la comprimento de rugosidade ($z_o$), e por la velocidade de fricção ($u$), da seguinte forma:
| $ V_t = \displaystyle\frac{2}{5} u \ln\left(\displaystyle\frac{ z_t }{ z_o }\right)$ |
| $ V_z = \displaystyle\frac{2}{5} u \ln\left(\displaystyle\frac{ z }{ z_o }\right)$ |
ID:(757, 2)
Redução da pressão na superfície (1)
Equação
O redução da pressão superficial ($q_z$) é a pressão por unidade de área pela qual ela diminui na superfície do corpo. É modelada como uma modificação do princípio de Bernoulli, caracterizada por la densidade do ar ($\rho_a$) e la velocidade do vento com altura ($V_z$), corrigindo a dinâmica com la fator de resposta dinâmica ($C_d$) e a geometria com o fator de forma aerodinâmica ($C_a$):
| $ q_b = \displaystyle\frac{1}{2} \rho_a V_b ^2 C_d C_a$ |
| $ q_z = \displaystyle\frac{1}{2} \rho_a V_z ^2 C_d C_a$ |
ID:(759, 1)
Redução da pressão na superfície (2)
Equação
O redução da pressão superficial ($q_z$) é a pressão por unidade de área pela qual ela diminui na superfície do corpo. É modelada como uma modificação do princípio de Bernoulli, caracterizada por la densidade do ar ($\rho_a$) e la velocidade do vento com altura ($V_z$), corrigindo a dinâmica com la fator de resposta dinâmica ($C_d$) e a geometria com o fator de forma aerodinâmica ($C_a$):
| $ q_t = \displaystyle\frac{1}{2} \rho_a V_t ^2 C_d C_a$ |
| $ q_z = \displaystyle\frac{1}{2} \rho_a V_z ^2 C_d C_a$ |
ID:(759, 2)
Pressão na superfície de um corpo (1)
Equação
O pressão na superfície ($p_z$) é igual a o pressão atmosférica ($p_0$) reduzido em o redução da pressão superficial ($q_z$):
| $ p_b = p_0 - q_b $ |
| $ p_z = p_0 - q_z $ |
ID:(776, 1)
Pressão na superfície de um corpo (2)
Equação
O pressão na superfície ($p_z$) é igual a o pressão atmosférica ($p_0$) reduzido em o redução da pressão superficial ($q_z$):
| $ p_t = p_0 - q_t $ |
| $ p_z = p_0 - q_z $ |
ID:(776, 2)
Diferença de pressão entre as bordas da parede
Equação
La diferença de pressão entre a borda inferior e superior ($\Delta p$) é o cálculo da diferença entre la pressão na borda inferior ($p_b$) e la pressão na borda superior ($p_t$):
| $ \Delta p = p_b - p_t $ |
ID:(775, 0)
Fluxo de vapor de água
Equação
A estimativa de la pressão na borda superior ($p_t$) é baseada na umidade que se desloca pelo espaço entre a parede e o revestimento, impulsionada por la diferença de pressão entre a borda inferior e superior ($\Delta p$). Supondo que la distância SIP e revestimento ($a$), la distância entre ripas ($b$), la altura vertical da parede ($h$) e la viscosidade ($\eta$):
| $ J_V = \displaystyle\frac{ a ^3 b }{12 \eta }\displaystyle\frac{ \Delta p }{ h }$ |
ID:(774, 0)