Utilisateur:
Séchage des murs
Storyboard 
Le séchage du mur se produit par évaporation de l'eau et son transport, soit par diffusion soit par flux d'air. La diffusion est un mécanisme très lent, car une zone d'humidité élevée se forme à la surface du mur, ce qui entrave l'évaporation supplémentaire et prolonge considérablement le temps pendant lequel le mur reste mouillé.
En revanche, le flux d'air est un mécanisme très efficace, car l'eau évaporée est éliminée par le flux d'air et remplacée par de l'air moins humide, qui peut à nouveau absorber plus d'eau lors de l'évaporation.
ID:(115, 0)
Pression à la surface
Concept
Le pression en surface ($p_z$), qui agit verticalement à la surface :
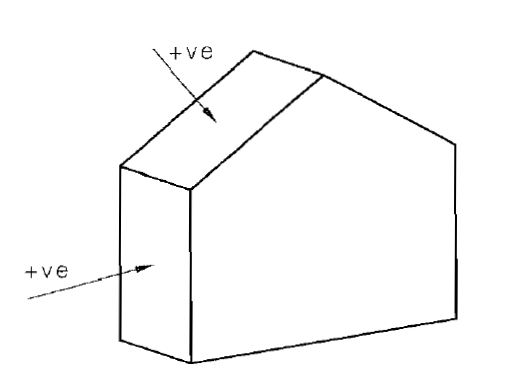
et est généralement inférieur à Le pression atmosphèrique ($p_0$) en raison des effets du déplacement de l'air de a densité de l'air ($\rho_a$) avec a vitesse du vent avec la hauteur ($V_z$).
Dans ce cas, nous pouvons le modéliser en utilisant l'équation de Bernoulli avec son terme d'énergie cinétique :
$\displaystyle\frac{1}{2} \rho_a V_Z^2$
Ce facteur est corrigé avec un facteur dépendant de la forme du corps, le facteur de forme aérodynamique ($C_a$), et un facteur provenant des fluctuations dues aux tourbillons de turbulence, le réduction de la pression superficielle ($q_z$), ce qui donne :
| $ q_z = \displaystyle\frac{1}{2} \rho_a V_z ^2 C_d C_a$ |
Ainsi, le pression en surface ($p_z$) peut être calculé, ce qui donne :
| $ p_z = p_0 - q_z $ |
ID:(768, 0)
Facteur de forme aérodynamique
Concept
L'effet du vent sur une structure dépend de la direction dans laquelle il frappe la surface. Si la direction du vent est représentée par une flèche, nous avons les situations suivantes :
| W | au vent (contre le vent) |
| S | latéral |
| L | sous le vent (avec le vent) |
| U | inclinaison du toit contre le vent |
| R | inclinaison du toit avec vent de travers |
| D | inclinaison du toit avec le vent |
Pour mieux comprendre ces concepts, des exemples fournis dans la norme AS/NZS 1170.2 peuvent être consultés :
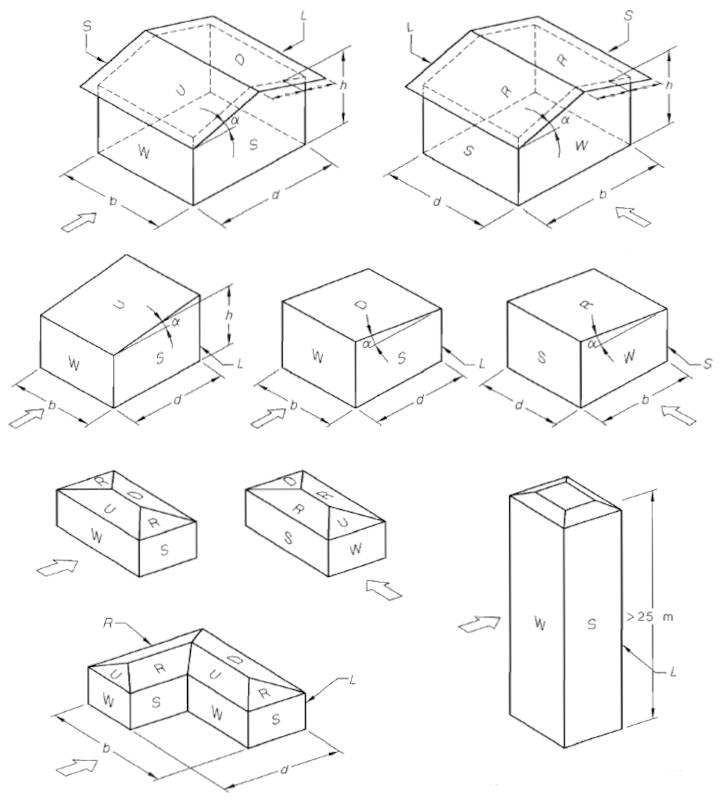
En résumé, le facteur de forme aérodynamique peut être modélisé par un facteur qui dépend de l'angle entre la normale à la surface et la direction du vent. Sur la base de données expérimentales provenant de différentes formes, ce facteur peut être approximé par une courbe de forme :
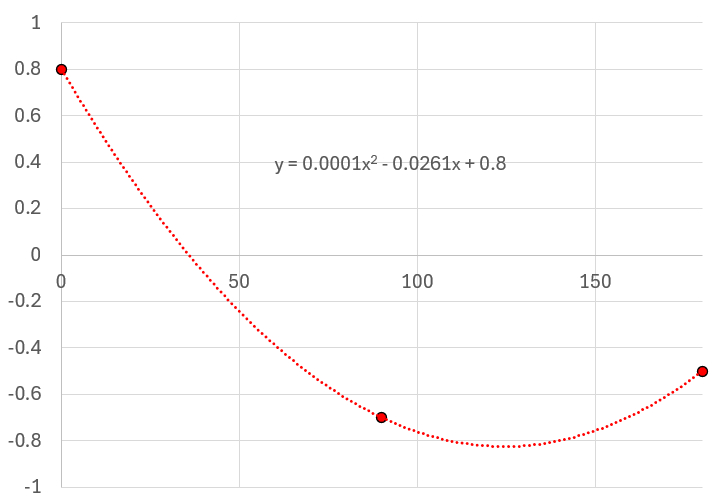
Il est important de comprendre que la fonction implique l'existence de zones de pression positive ainsi que de zones de pression négative, correspondant à des zones où littéralement, le vent aspire.
ID:(760, 0)
Modèle
Concept
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ C_a = 0.3445 \theta ^2 - 1.4961 \theta + 0.8$
C_a = 0.3445* theta ^2 - 1.4961* theta + 0.8
$ \Delta p = p_b - p_t $
Dp = p_b - p_t
$ J_V = \displaystyle\frac{ a ^3 b }{12 \eta }\displaystyle\frac{ \Delta p }{ h }$
J_V = a ^3* b * Dp /(12* eta * h)
$ p_b = p_0 - q_b $
p_z = p_0 - q_z
$ p_t = p_0 - q_t $
p_z = p_0 - q_z
$ q_b = \displaystyle\frac{1}{2} \rho_a V_b ^2 C_d C_a$
q_z = rho_a * V_z ^2* C_d * C_a /2
$ q_t = \displaystyle\frac{1}{2} \rho_a V_t ^2 C_d C_a$
q_z = rho_a * V_z ^2* C_d * C_a /2
$ V_b = \displaystyle\frac{2}{5} u \ln\left(\displaystyle\frac{ z_b }{ z_o }\right)$
V_z = 2* u * log( z / z_o )/5
$ V_t = \displaystyle\frac{2}{5} u \ln\left(\displaystyle\frac{ z_t }{ z_o }\right)$
V_z = 2* u * log( z / z_o )/5
ID:(773, 0)
Modèle de facteur de forme aérodynamique
Équation
Le facteur de forme aérodynamique ($C_a$) peut être modélisé en fonction de le angle du vent ($\theta$) pour estimer les contributions à la pression des différentes surfaces de l'objet. Ce modèle est basé sur des constantes dérivées de mesures effectuées sur différents objets:
| $ C_a = 0.3445 \theta ^2 - 1.4961 \theta + 0.8$ |
ID:(761, 0)
Vitesse avec hauteur (1)
Équation
A vitesse du vent avec la hauteur ($V_z$) dépend de a hauteur au dessus du sol ($z$). En général, il est pratiquement nul à la surface et atteint la valeur indiquée dans les rapports météorologiques à une hauteur de 10 mètres. Sa variation est influencée par la rugosité du terrain, exprimée par a longueur de rugosité ($z_o$), et par a vitesse de friction ($u$), comme suit :
| $ V_b = \displaystyle\frac{2}{5} u \ln\left(\displaystyle\frac{ z_b }{ z_o }\right)$ |
| $ V_z = \displaystyle\frac{2}{5} u \ln\left(\displaystyle\frac{ z }{ z_o }\right)$ |
ID:(757, 1)
Vitesse avec hauteur (2)
Équation
A vitesse du vent avec la hauteur ($V_z$) dépend de a hauteur au dessus du sol ($z$). En général, il est pratiquement nul à la surface et atteint la valeur indiquée dans les rapports météorologiques à une hauteur de 10 mètres. Sa variation est influencée par la rugosité du terrain, exprimée par a longueur de rugosité ($z_o$), et par a vitesse de friction ($u$), comme suit :
| $ V_t = \displaystyle\frac{2}{5} u \ln\left(\displaystyle\frac{ z_t }{ z_o }\right)$ |
| $ V_z = \displaystyle\frac{2}{5} u \ln\left(\displaystyle\frac{ z }{ z_o }\right)$ |
ID:(757, 2)
Réduction de la pression sur la surface (1)
Équation
Le réduction de la pression superficielle ($q_z$) est la pression par unité de surface par laquelle elle diminue sur la surface du corps. Elle est modélisée comme une modification du principe de Bernoulli, caractérisée par a densité de l'air ($\rho_a$) et a vitesse du vent avec la hauteur ($V_z$), corrigeant la dynamique avec a facteur de réponse dynamique ($C_d$) et la géométrie avec le facteur de forme aérodynamique ($C_a$) :
| $ q_b = \displaystyle\frac{1}{2} \rho_a V_b ^2 C_d C_a$ |
| $ q_z = \displaystyle\frac{1}{2} \rho_a V_z ^2 C_d C_a$ |
ID:(759, 1)
Réduction de la pression sur la surface (2)
Équation
Le réduction de la pression superficielle ($q_z$) est la pression par unité de surface par laquelle elle diminue sur la surface du corps. Elle est modélisée comme une modification du principe de Bernoulli, caractérisée par a densité de l'air ($\rho_a$) et a vitesse du vent avec la hauteur ($V_z$), corrigeant la dynamique avec a facteur de réponse dynamique ($C_d$) et la géométrie avec le facteur de forme aérodynamique ($C_a$) :
| $ q_t = \displaystyle\frac{1}{2} \rho_a V_t ^2 C_d C_a$ |
| $ q_z = \displaystyle\frac{1}{2} \rho_a V_z ^2 C_d C_a$ |
ID:(759, 2)
Pression à la surface d'un corps (1)
Équation
Le pression en surface ($p_z$) est égal à Le pression atmosphèrique ($p_0$) réduit de le réduction de la pression superficielle ($q_z$) :
| $ p_b = p_0 - q_b $ |
| $ p_z = p_0 - q_z $ |
ID:(776, 1)
Pression à la surface d'un corps (2)
Équation
Le pression en surface ($p_z$) est égal à Le pression atmosphèrique ($p_0$) réduit de le réduction de la pression superficielle ($q_z$) :
| $ p_t = p_0 - q_t $ |
| $ p_z = p_0 - q_z $ |
ID:(776, 2)
Différence de pression entre les bords des murs
Équation
A différence de pression entre le bord inférieur et supérieur ($\Delta p$) est calculé à partir de la différence entre a pression sur le bord inférieur ($p_b$) et a pression sur le bord supérieur ($p_t$) :
| $ \Delta p = p_b - p_t $ |
ID:(775, 0)
Flux de vapeur d'eau
Équation
L'estimation de a pression sur le bord supérieur ($p_t$) est basée sur l'humidité qui se déplace à travers l'espace entre le mur et le revêtement, entraînée par a différence de pression entre le bord inférieur et supérieur ($\Delta p$). En supposant que a distance SIP et revêtement ($a$), a distance entre les lattes ($b$), a hauteur du mur vertical ($h$) et a viscosité ($\eta$) :
| $ J_V = \displaystyle\frac{ a ^3 b }{12 \eta }\displaystyle\frac{ \Delta p }{ h }$ |
ID:(774, 0)