Utilisateur:
Mouiller le mur
Storyboard 
À chaque fois qu'il pleut, l'humidité relative atteint des valeurs proches ou égales à 100%. Cela signifie que l'air est saturé d'eau, et toute surface absorbera des molécules jusqu'à ce qu'un film d'eau se forme. Ce film aura tendance à glisser sous l'effet de la gravité, commençant à "goutter" le long du mur. De plus, il existe un film d'environ 120 nm qui reste même après l'arrêt de la pluie et doit être enlevé par le processus de séchage pour éviter la formation de moisissures, ce qui pourrait dégrader le mur.
ID:(113, 0)
Air saturé
Concept
Pendant une pluie, les gouttes tombent vers le sol. Chaque goutte présente une surface d'eau en contact avec l'air. Les molécules d'eau peuvent se détacher des gouttes et former ce que nous appelons de la vapeur d'eau.
S'il y en a beaucoup, il n'est pas impossible que ces molécules soient de nouveau absorbées par les gouttes. Finalement, il existe un équilibre entre les molécules qui parviennent à s'échapper et celles qui sont réabsorbées par les gouttes. Lorsque le nombre de molécules par volume atteint cette situation, on dit que l'air est saturé d'eau.
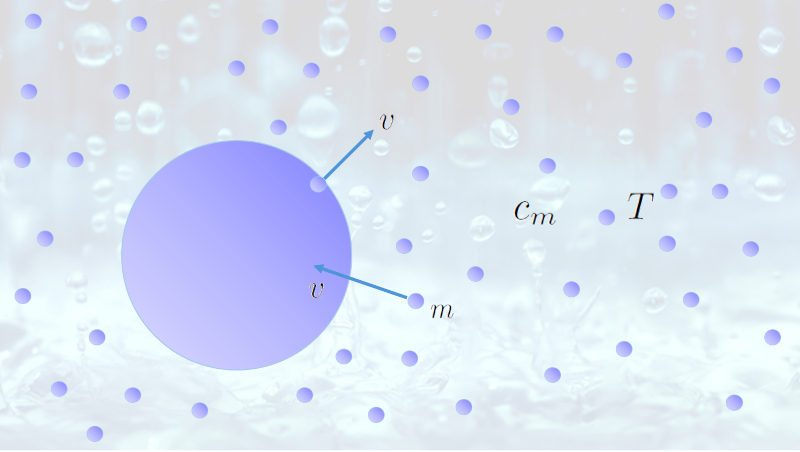
Ce qui vient d'être décrit peut être modélisé en obtenant le pression saturée ($p_s$), qui dépend de le pression de référence ($p_{ref}$), a chaleur spécifique molaire d'évaporation ($l_m$), le constante du gaz universel ($R$) et le température ($T$), grâce à l'équation
| $ p_s = p_{ref} e^{- l_m / R T }$ |
qui correspond à la pression de vapeur d'eau pour le cas où l'air est saturé.
En utilisant les équations des gaz où Le nombre de moles ($n$) est exprimé par le volume ($V$) et a concentration molaire saturée ($c_s$) est exprimé par le température ($T$) grâce à
| $ p_s = c_s R T $ |
Dans le cas où l'air est saturé, le humidité relative ($RH$) est à 100%, et ainsi a concentration molaire saturée ($c_s$) est égal à A concentration molaire ($c_m$) étant donné que
| $ RH = \displaystyle\frac{ c_m }{ c_s }$ |
nous obtenons a concentration molaire ($c_m$) de l'air pendant l'événement de pluie.
ID:(798, 0)
Mouvement des molécules d'eau
Concept
Le pression saturée ($p_s$) dépend de a chaleur spécifique molaire d'évaporation ($l_m$) et le température ($T$), ainsi que des constantes le pression de référence ($p_{ref}$) et le constante du gaz universel ($R$):
 $$ |
ID:(799, 0)
Absorption d'eau murale
Concept
Si près de l'air saturé en eau existe une surface comme un mur, les molécules d'eau s'y colleront. Cela correspond à un flux continu tant que un humidité relative ($RH$) reste égal à 100%. Les mesures montrent que la couche croît alors que l'eau s'écoule par gravité, laissant le bord inférieur du mur. Cependant, en raison de la cohésion des molécules d'eau, une couche un épaisseur de couche ($d$) se forme d'une épaisseur de l'ordre de $120 nm$ :
On estime le élément de volume ($\Delta V$) à partir de le épaisseur de couche ($d$) et a section ($S$) grâce à :
| $ \Delta V = S d $ |
Pour une section ($S$) de surface en mètre carré avec le épaisseur de couche ($d$) égal à $120 nm$, on obtient une section ($S$) égal à $1.2e-7 m^2$. On peut calculer le variation du nombre de moles ($\Delta n$) avec a densité ($\rho$) égal à $10^3 kg/m^3$, a masse molaire ($M_m$) égal à $0.018 kg/ml$ et le élément de volume ($\Delta V$) avec :
| $ \Delta n = \displaystyle\frac{ \rho \Delta V }{ M_m }$ |
ce qui donne $6.67e-3 mol$. Avec un débit de plusieurs moles par mètre carré et par seconde, il faut une fraction de seconde pour que le mur forme la couche d'eau.
Tout mur entrant en contact avec de l'air saturé s'humidifie en quelques secondes
ID:(800, 0)
Modèle
Concept
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ D = \displaystyle\frac{1}{3} v l $
D = v * l /3
$ \Delta n = \displaystyle\frac{ \rho \Delta V }{ M_m }$
Dn = rho * DV / M_m
$ \Delta V = S d $
DV = S * d
$ j_n = - D \displaystyle\frac{ \Delta c_m }{ \Delta x }$
j_n = - D * Dc_m / Dx
$j_n = \displaystyle\frac{1}{6} c_m v $
j_n = c_m * v /6
$ J_n = \displaystyle\frac{ \Delta c_m }{ \Delta t }$
J_n = Dc_m / Dt
$ J_n = j_n S $
J_n = j_n * S
$l = \displaystyle\frac{1}{\sqrt{2} N_A c_m \sigma_0 }$
l = 1/(sqrt(2)* N_A * c_m * sigma_0 )
$ p = c_m R T $
p = c_m * R * T
$ p_s = c_s R T $
p_s = c_s * R * T
$ p_s = p_{ref} e^{- l_m / R T }$
p_s = p_ref * exp(- l_m /( R * T ))
$ RH = \displaystyle\frac{ c_m }{ c_s }$
RH = c_m / c_s
$ RH = \displaystyle\frac{ p }{ p_s }$
RH = p / p_s
$ \sigma_0 = 4 \pi r ^2$
sigma_0 = 4* pi * r ^2
$v = \sqrt{\displaystyle\frac{8 k_B T }{ \pi m }}$
v = sqrt(8* k_B * T /( pi * m ))
ID:(773, 0)
Pression saturée
Équation
Le pression saturée ($p_s$) dépend de a chaleur spécifique molaire d'évaporation ($l_m$) et le température ($T$), ainsi que des constantes le pression de référence ($p_{ref}$) et le constante du gaz universel ($R$):
| $ p_s = p_{ref} e^{- l_m / R T }$ |
ID:(782, 0)
Pression molaire saturée et concentration
Équation
Dans le cas d'un gaz idéal, le pression saturée ($p_s$) qui satisfait à A concentration molaire saturée ($c_s$), le température ($T$) et le constante du gaz universel ($R$):
| $ p_s = c_s R T $ |
ID:(781, 0)
Pression et concentration molaire
Équation
Dans le cas d'un gaz idéal, le pression ($p$) qui satisfait à A concentration molaire ($c_m$), le température ($T$) et le constante du gaz universel ($R$):
| $ p = c_m R T $ |
ID:(780, 0)
Humidité relative en fonction de la pression
Équation
Le humidité relative ($RH$) peut être calculé à l'aide de le pression ($p$) et le pression saturée ($p_s$) grâce à la formule suivante :
| $ RH = \displaystyle\frac{ p }{ p_s }$ |
ID:(778, 0)
Humidité relative en fonction de la concentration
Équation
Le humidité relative ($RH$) peut être calculé à l'aide de a concentration molaire ($c_m$) et a concentration molaire saturée ($c_s$) grâce à la formule suivante :
| $ RH = \displaystyle\frac{ c_m }{ c_s }$ |
ID:(779, 0)
Flux et densité de flux molaire
Équation
A flux molaire ($J_n$) dépend de a densité de flux molaire ($j_n$) et a section ($S$), comme indiqué ci-dessous :
| $ J_n = j_n S $ |
ID:(784, 0)
Flux molaire
Équation
A flux molaire ($J_n$) dépend de le différence de concentration molaire ($\Delta c_m$) et le intervalle de temps ($\Delta t$), comme indiqué ci-dessous :
| $ J_n = \displaystyle\frac{ \Delta c_m }{ \Delta t }$ |
ID:(795, 0)
Densité de flux
Équation
A densité de flux molaire ($j_n$) dépend de la concentration de particules, qui est calculée à partir de a concentration molaire ($c_m$) en multipliant par a vitesse des molécules ($v$), selon la relation suivante :
| $j_n = \displaystyle\frac{1}{6} c_m v $ |
ID:(791, 0)
Vitesse des molécules
Équation
A vitesse des molécules ($v$) peut être calculé à partir de a constante de Boltzmann ($k_B$), le température ($T$), a pi ($\pi$) et a masse moléculaire ($m$) en utilisant la relation suivante :
| $v = \sqrt{\displaystyle\frac{8 k_B T }{ \pi m }}$ |
ID:(789, 0)
Loi de Fick molaire
Équation
A densité de flux molaire ($j_n$) dépend de a constante de diffusion ($D$), qui à son tour dépend de le différence de concentration molaire ($\Delta c_m$) et a distance de diffusion ($\Delta x$) :
| $ j_n = - D \displaystyle\frac{ \Delta c_m }{ \Delta x }$ |
ID:(793, 0)
Coefficient de diffusion
Équation
A constante de diffusion ($D$) est modélisé comme des molécules représentées par des sphères qui se déplacent avec a vitesse des molécules ($v$) Un chemin libre ($l$), comme suit :
| $ D = \displaystyle\frac{1}{3} v l $ |
ID:(786, 0)
Chemin libre
Équation
A vitesse des molécules ($v$) peut être calculé à partir de a constante de Boltzmann ($k_B$), le température ($T$), a pi ($\pi$) et a section efficace totale de diffusion ($\sigma_0$) en utilisant la relation suivante :
| $l = \displaystyle\frac{1}{\sqrt{2} N_A c_m \sigma_0 }$ |
ID:(790, 0)
Section efficace totale de diffusion
Équation
A section efficace totale de diffusion ($\sigma_0$) est, dans le cas de collisions entre sphères rigides, égal à une fonction de a rayon de la molécule ($r$) :
| $ \sigma_0 = 4 \pi r ^2$ |
ID:(788, 0)
Variation des grains de beauté
Équation
Le variation du nombre de moles ($\Delta n$) dépend de a densité ($\rho$), le élément de volume ($\Delta V$) et a masse molaire ($M_m$), comme indiqué ci-dessous :
| $ \Delta n = \displaystyle\frac{ \rho \Delta V }{ M_m }$ |
ID:(796, 0)
Volume de couche
Équation
Le élément de volume ($\Delta V$) dépend de a section ($S$) et le épaisseur de couche ($d$), comme indiqué ci-dessous :
| $ \Delta V = S d $ |
ID:(797, 0)