User:
Wetting of the wall
Storyboard 
Every time it rains, the relative humidity reaches values close to or equal to 100%. This means that the air is saturated with water, and any surface will absorb molecules until it forms a water film. This film will tend to slide due to gravity, starting to "drip" down the wall. Additionally, there is a film of about 120 nm that remains even after the rain stops and must be removed through the drying process to prevent the formation of mold, which can degrade the wall.
ID:(113, 0)
Saturated air
Concept
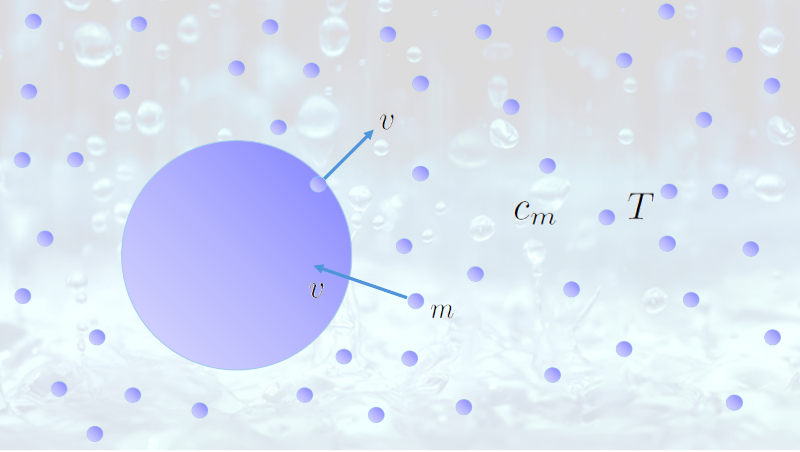
During rain, drops fall towards the ground. Each drop presents a surface of water in contact with the air. Water molecules can detach from the drops and form what we call water vapor.
If there are many of these molecules, there is a non-zero probability that they will be reabsorbed by the drops. Ultimately, there is a balance between the molecules that manage to escape and those that are reabsorbed by the drops. When the number of molecules per volume reaches this situation, we say that the air is saturated with water.
What has been described can be modeled by obtaining the saturated pressure ($p_s$), which depends on the reference pressure ($p_{ref}$), the molar specific heat of evaporation ($l_m$), the universal gas constant ($R$), and the temperature ($T$), through the equation
| $ p_s = p_{ref} e^{- l_m / R T }$ |
which corresponds to the vapor pressure for the case when the air is saturated.
Using the gas equations where the number of moles ($n$) is expressed by the volume ($V$) and the saturated molar concentration ($c_s$) is expressed by the temperature ($T$) through
| $ p_s = c_s R T $ |
In the case where the air is saturated, the relative humidity ($RH$) is 100%, and thus the saturated molar concentration ($c_s$) is equal to the molar concentration ($c_m$) since
| $ RH = \displaystyle\frac{ c_m }{ c_s }$ |
we obtain the molar concentration ($c_m$) from the air during the rain event.
ID:(798, 0)
Movement of water molecules
Concept
The saturated pressure ($p_s$) depends on the molar specific heat of evaporation ($l_m$) and the temperature ($T$), as well as the constants the reference pressure ($p_{ref}$) and the universal gas constant ($R$):
 $$ |
ID:(799, 0)
Wall water absorption
Concept
If there is a surface near saturated water vapor, such as a wall, water molecules will adhere to it. This corresponds to a continuous flow as long as a relative humidity ($RH$) remains equal to 100%. Measurements show that the layer grows as water flows by gravity, leaving the bottom edge of the wall. However, due to the cohesion of water molecules, a layer a layer thickness ($d$) forms with a thickness on the order of $120 nm$:
the volume element ($\Delta V$) is estimated from the layer thickness ($d$) and the section ($S$) through:
| $ \Delta V = S d $ |
For a section ($S$) square meters with the layer thickness ($d$) equal to $120 nm$, we obtain a section ($S$) equal to $1.2e-7 m^2$. The variation of the number of moles ($\Delta n$) can be calculated with the density ($\rho$) equal to $10^3 kg/m^3$, the molar mass ($M_m$) equal to $0.018 kg/ml$ and the volume element ($\Delta V$) with:
| $ \Delta n = \displaystyle\frac{ \rho \Delta V }{ M_m }$ |
resulting in $6.67e-3 mol$. With a flow of several moles per square meter per second, it takes a fraction of a second for the wall to form the water layer.
Any wall that comes into contact with saturated air becomes damp in fractions of seconds
ID:(800, 0)
Model
Concept
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ D = \displaystyle\frac{1}{3} v l $
D = v * l /3
$ \Delta n = \displaystyle\frac{ \rho \Delta V }{ M_m }$
Dn = rho * DV / M_m
$ \Delta V = S d $
DV = S * d
$ j_n = - D \displaystyle\frac{ \Delta c_m }{ \Delta x }$
j_n = - D * Dc_m / Dx
$j_n = \displaystyle\frac{1}{6} c_m v $
j_n = c_m * v /6
$ J_n = \displaystyle\frac{ \Delta c_m }{ \Delta t }$
J_n = Dc_m / Dt
$ J_n = j_n S $
J_n = j_n * S
$l = \displaystyle\frac{1}{\sqrt{2} N_A c_m \sigma_0 }$
l = 1/(sqrt(2)* N_A * c_m * sigma_0 )
$ p = c_m R T $
p = c_m * R * T
$ p_s = c_s R T $
p_s = c_s * R * T
$ p_s = p_{ref} e^{- l_m / R T }$
p_s = p_ref * exp(- l_m /( R * T ))
$ RH = \displaystyle\frac{ c_m }{ c_s }$
RH = c_m / c_s
$ RH = \displaystyle\frac{ p }{ p_s }$
RH = p / p_s
$ \sigma_0 = 4 \pi r ^2$
sigma_0 = 4* pi * r ^2
$v = \sqrt{\displaystyle\frac{8 k_B T }{ \pi m }}$
v = sqrt(8* k_B * T /( pi * m ))
ID:(773, 0)
Saturated pressure
Equation
The saturated pressure ($p_s$) depends on the molar specific heat of evaporation ($l_m$) and the temperature ($T$), as well as the constants the reference pressure ($p_{ref}$) and the universal gas constant ($R$):
| $ p_s = p_{ref} e^{- l_m / R T }$ |
ID:(782, 0)
Saturated molar pressure and concentration
Equation
In the case of an ideal gas, the saturated pressure ($p_s$) that satisfies the saturated molar concentration ($c_s$), the temperature ($T$), and the universal gas constant ($R$):
| $ p_s = c_s R T $ |
ID:(781, 0)
Pressure and molar concentration
Equation
In the case of an ideal gas, the pressure ($p$) that satisfies the molar concentration ($c_m$), the temperature ($T$), and the universal gas constant ($R$):
| $ p = c_m R T $ |
ID:(780, 0)
Relative humidity as a function of pressure
Equation
The relative humidity ($RH$) can be calculated using the pressure ($p$) and the saturated pressure ($p_s$) through the following formula:
| $ RH = \displaystyle\frac{ p }{ p_s }$ |
ID:(778, 0)
Relative humidity as a function of concentration
Equation
The relative humidity ($RH$) can be calculated using the molar concentration ($c_m$) and the saturated molar concentration ($c_s$) through the following formula:
| $ RH = \displaystyle\frac{ c_m }{ c_s }$ |
ID:(779, 0)
Flow and molar flow density
Equation
The molar flow ($J_n$) depends on the molar flow density ($j_n$) and the section ($S$), as shown below:
| $ J_n = j_n S $ |
ID:(784, 0)
Molar flow
Equation
The molar flow ($J_n$) depends on the molar concentration difference ($\Delta c_m$) and the time interval ($\Delta t$), as shown below:
| $ J_n = \displaystyle\frac{ \Delta c_m }{ \Delta t }$ |
ID:(795, 0)
Flux density
Equation
The molar flow density ($j_n$) depends on the particle concentration, calculated from the molar concentration ($c_m$) by multiplying by the speed of molecules ($v$), according to the following relationship:
| $j_n = \displaystyle\frac{1}{6} c_m v $ |
ID:(791, 0)
Speed of molecules
Equation
The speed of molecules ($v$) can be calculated from the boltzmann constant ($k_B$), the temperature ($T$), the pi ($\pi$), and the molecule mass ($m$) using the following relationship:
| $v = \sqrt{\displaystyle\frac{8 k_B T }{ \pi m }}$ |
ID:(789, 0)
Molar Fick's Law
Equation
The molar flow density ($j_n$) depends on the diffusion constant ($D$), which in turn depends on the molar concentration difference ($\Delta c_m$) and the diffusion distance ($\Delta x$):
| $ j_n = - D \displaystyle\frac{ \Delta c_m }{ \Delta x }$ |
ID:(793, 0)
Diffusion coefficient
Equation
The diffusion constant ($D$) is modeled as molecules represented by spheres that travel with the speed of molecules ($v$) A free path ($l$), as follows
| $ D = \displaystyle\frac{1}{3} v l $ |
ID:(786, 0)
Free path
Equation
The free path ($l$) depends on the particle concentration, calculated from the molar concentration ($c_m$) by multiplying by the avogadro's number ($N_A$), and the total scattering cross section ($\sigma_0$), according to the following relationship:
| $l = \displaystyle\frac{1}{\sqrt{2} N_A c_m \sigma_0 }$ |
ID:(790, 0)
Total scattering cross section
Equation
The total scattering cross section ($\sigma_0$) is, in the case of collisions between rigid spheres, equal to a function of the radius of the molecule ($r$):
| $ \sigma_0 = 4 \pi r ^2$ |
ID:(788, 0)
Variation of moles
Equation
The variation of the number of moles ($\Delta n$) depends on the density ($\rho$), the volume element ($\Delta V$), and the molar mass ($M_m$), as shown below:
| $ \Delta n = \displaystyle\frac{ \rho \Delta V }{ M_m }$ |
ID:(796, 0)
Layer volume
Equation
The volume element ($\Delta V$) depends on the section ($S$) and the layer thickness ($d$), as shown below:
| $ \Delta V = S d $ |
ID:(797, 0)