Benützer:
Benetzung der Wand
Storyboard 
Immer wenn es regnet, steigt die relative Luftfeuchtigkeit auf Werte nahe oder gleich 100 %. Das bedeutet, dass die Luft gesättigt ist mit Wasser, und jede Oberfläche wird Moleküle absorbieren, bis sich ein Wasserfilm bildet. Dieser Film neigt dazu, aufgrund der Schwerkraft zu rutschen und beginnt an der Wand zu "tropfen". Zusätzlich gibt es einen Film von etwa 120 nm, der auch nach dem Regen bestehen bleibt und durch den Trocknungsprozess entfernt werden muss, um die Bildung von Schimmel zu verhindern, der die Wand beschädigen könnte.
ID:(113, 0)
Gesättigte Luft
Konzept
Während des Regens fallen die Tropfen auf den Boden. Jeder Tropfen hat eine Oberfläche aus Wasser, die mit der Luft in Kontakt steht. Wasser-Moleküle können sich von den Tropfen lösen und bilden das, was wir Wasserdampf nennen.
Wenn es viele dieser Moleküle gibt, ist die Wahrscheinlichkeit nicht null, dass sie von den Tropfen wieder aufgenommen werden. Letztendlich besteht ein Gleichgewicht zwischen den Molekülen, die entkommen können, und denen, die von den Tropfen wieder aufgenommen werden. Wenn die Anzahl der Moleküle pro Volumen diese Situation erreicht, sagen wir, dass die Luft mit Wasser gesättigt ist.
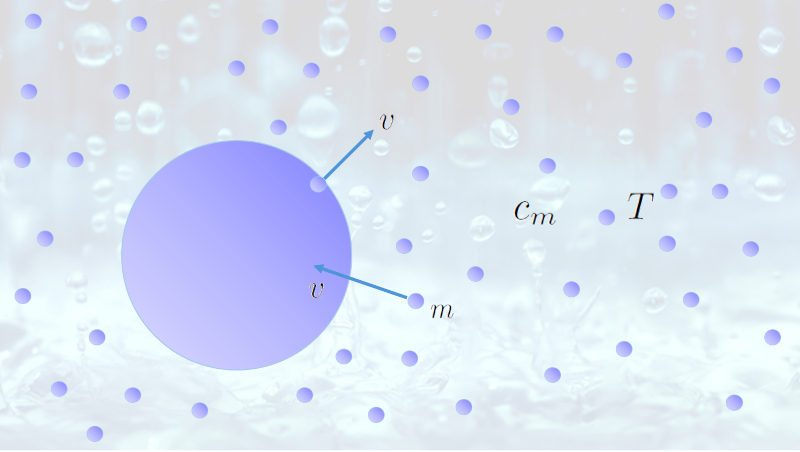
Was beschrieben wurde, kann modelliert werden, indem man der Gesättigter Druck ($p_s$) erhält, das von der Referenzdruck ($p_{ref}$), die Molare spezifische Verdampfungswärme ($l_m$), der Universelle Gas Konstante ($R$) und der Temperatur ($T$) abhängt, durch die Gleichung
| $ p_s = p_{ref} e^{- l_m / R T }$ |
die dem Dampfdruck für den Fall entspricht, dass die Luft gesättigt ist.
Mit den Gasgleichungen, in denen der Anzahl der Mol ($n$) durch der Volumen ($V$) und die Gesättigte molare Konzentration ($c_s$) durch der Temperatur ($T$) ausgedrückt wird, durch
| $ p_s = c_s R T $ |
Im Falle einer gesättigten Luft beträgt der Relative Luftfeuchtigkeit ($RH$) 100%, und daher ist die Gesättigte molare Konzentration ($c_s$) gleich die Molare Konzentration ($c_m$), da
| $ RH = \displaystyle\frac{ c_m }{ c_s }$ |
erhalten wir die Molare Konzentration ($c_m$) aus der Luft während des Regenereignisses.
ID:(798, 0)
Bewegung von Wassermolekülen
Konzept
Der Gesättigter Druck ($p_s$) hängt von die Molare spezifische Verdampfungswärme ($l_m$) und der Temperatur ($T$) ab, sowie von den Konstanten der Referenzdruck ($p_{ref}$) und der Universelle Gas Konstante ($R$):
 $$ |
ID:(799, 0)
Wandwasseraufnahme
Konzept
Wenn sich in der Nähe von gesättigter Luft mit Wasser eine Oberfläche wie eine Wand befindet, werden die Wassermoleküle daran haften. Dies entspricht einem kontinuierlichen Fluss, solange ein Relative Luftfeuchtigkeit ($RH$) gleich 100% bleibt. Messungen zeigen, dass die Schicht wächst, während das Wasser durch Schwerkraft abfließt und den unteren Rand der Wand zurücklässt. Aufgrund der Kohäsion der Wassermoleküle bildet sich jedoch eine Schicht ein Schichtdicke ($d$) mit einer Dicke von etwa $120 nm$:
der Volumenelement ($\Delta V$) wird aus der Schichtdicke ($d$) und die Sektion ($S$) abgeschätzt durch:
| $ \Delta V = S d $ |
Für eine Sektion ($S$) Quadratmeter mit der Schichtdicke ($d$) gleich $120 nm$ ergibt sich eine Sektion ($S$) gleich $1.2e-7 m^2$. Der Variation der Molzahl ($\Delta n$) kann mit die Dichte ($\rho$) gleich $10^3 kg/m^3$, die Molekülmasse ($M_m$) gleich $0.018 kg/ml$ und der Volumenelement ($\Delta V$) mit:
| $ \Delta n = \displaystyle\frac{ \rho \Delta V }{ M_m }$ |
berechnet werden, was $6.67e-3 mol$ ergibt. Bei einem Fluss von mehreren Mol pro Quadratmeter und Sekunde dauert es einen Bruchteil einer Sekunde, bis die Wand die Wasserschicht bildet.
Jede Wand, die mit gesättigter Luft in Kontakt kommt, befeuchtet sich in Sekundenbruchteilen
ID:(800, 0)
Modell
Konzept
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ D = \displaystyle\frac{1}{3} v l $
D = v * l /3
$ \Delta n = \displaystyle\frac{ \rho \Delta V }{ M_m }$
Dn = rho * DV / M_m
$ \Delta V = S d $
DV = S * d
$ j_n = - D \displaystyle\frac{ \Delta c_m }{ \Delta x }$
j_n = - D * Dc_m / Dx
$j_n = \displaystyle\frac{1}{6} c_m v $
j_n = c_m * v /6
$ J_n = \displaystyle\frac{ \Delta c_m }{ \Delta t }$
J_n = Dc_m / Dt
$ J_n = j_n S $
J_n = j_n * S
$l = \displaystyle\frac{1}{\sqrt{2} N_A c_m \sigma_0 }$
l = 1/(sqrt(2)* N_A * c_m * sigma_0 )
$ p = c_m R T $
p = c_m * R * T
$ p_s = c_s R T $
p_s = c_s * R * T
$ p_s = p_{ref} e^{- l_m / R T }$
p_s = p_ref * exp(- l_m /( R * T ))
$ RH = \displaystyle\frac{ c_m }{ c_s }$
RH = c_m / c_s
$ RH = \displaystyle\frac{ p }{ p_s }$
RH = p / p_s
$ \sigma_0 = 4 \pi r ^2$
sigma_0 = 4* pi * r ^2
$v = \sqrt{\displaystyle\frac{8 k_B T }{ \pi m }}$
v = sqrt(8* k_B * T /( pi * m ))
ID:(773, 0)
Gesättigter Druck
Gleichung
Der Gesättigter Druck ($p_s$) hängt von die Molare spezifische Verdampfungswärme ($l_m$) und der Temperatur ($T$) ab, sowie von den Konstanten der Referenzdruck ($p_{ref}$) und der Universelle Gas Konstante ($R$):
| $ p_s = p_{ref} e^{- l_m / R T }$ |
ID:(782, 0)
Gesättigter molarer Druck und Konzentration
Gleichung
Im Fall eines idealen Gases, der Gesättigter Druck ($p_s$), das die Gesättigte molare Konzentration ($c_s$), der Temperatur ($T$) und der Universelle Gas Konstante ($R$) erfüllt:
| $ p_s = c_s R T $ |
ID:(781, 0)
Druck und molare Konzentration
Gleichung
Im Fall eines idealen Gases, der Druck ($p$), das die Molare Konzentration ($c_m$), der Temperatur ($T$) und der Universelle Gas Konstante ($R$) erfüllt:
| $ p = c_m R T $ |
ID:(780, 0)
Relative Luftfeuchtigkeit als Funktion des Drucks
Gleichung
Der Relative Luftfeuchtigkeit ($RH$) kann mithilfe von der Druck ($p$) und der Gesättigter Druck ($p_s$) durch folgende Formel berechnet werden:
| $ RH = \displaystyle\frac{ p }{ p_s }$ |
ID:(778, 0)
Relative Luftfeuchtigkeit als Funktion der Konzentration
Gleichung
Der Relative Luftfeuchtigkeit ($RH$) kann mithilfe von die Molare Konzentration ($c_m$) und die Gesättigte molare Konzentration ($c_s$) durch folgende Formel berechnet werden:
| $ RH = \displaystyle\frac{ c_m }{ c_s }$ |
ID:(779, 0)
Durchfluss und molare Durchflussdichte
Gleichung
Die Molarer Fluss ($J_n$) hängt von die Molare Flussdichte ($j_n$) und die Sektion ($S$) ab, wie unten gezeigt:
| $ J_n = j_n S $ |
ID:(784, 0)
Molarer Fluss
Gleichung
Die Molarer Fluss ($J_n$) hängt von der Molarer Konzentrationsunterschied ($\Delta c_m$) und der Zeitintervall ($\Delta t$) ab, wie unten gezeigt:
| $ J_n = \displaystyle\frac{ \Delta c_m }{ \Delta t }$ |
ID:(795, 0)
Flussdichte
Gleichung
Die Molare Flussdichte ($j_n$) hängt von der Partikelkonzentration ab, die durch Multiplikation von die Molare Konzentration ($c_m$) mit die Geschwindigkeit von Molekülen ($v$) gemäß der folgenden Beziehung berechnet wird:
| $j_n = \displaystyle\frac{1}{6} c_m v $ |
ID:(791, 0)
Geschwindigkeit von Molekülen
Gleichung
Die Geschwindigkeit von Molekülen ($v$) kann aus die Boltzmann-Konstante ($k_B$), der Temperatur ($T$), die Pi ($\pi$) und die Molekülmasse ($m$) mithilfe der folgenden Beziehung berechnet werden:
| $v = \sqrt{\displaystyle\frac{8 k_B T }{ \pi m }}$ |
ID:(789, 0)
Molares Fick-Gesetz
Gleichung
Die Molare Flussdichte ($j_n$) hängt von die Diffusionskonstante ($D$) ab, das wiederum von der Molarer Konzentrationsunterschied ($\Delta c_m$) und die Diffusionsentfernung ($\Delta x$) abhängt:
| $ j_n = - D \displaystyle\frac{ \Delta c_m }{ \Delta x }$ |
ID:(793, 0)
Diffusionskoeffizient
Gleichung
Die Diffusionskonstante ($D$) wird modelliert als Moleküle, die durch Kugeln dargestellt werden und sich mit die Geschwindigkeit von Molekülen ($v$) Ein Freier Weg ($l$) bewegen, wie folgt:
| $ D = \displaystyle\frac{1}{3} v l $ |
ID:(786, 0)
Freier Weg
Gleichung
Der Freier Weg ($l$) hängt von der Partikelkonzentration ab, die durch Multiplikation von die Molare Konzentration ($c_m$) mit der Avogadros Nummer ($N_A$) und die Gesamtwirkungsquerschnitt für Streuung ($\sigma_0$) gemäß der folgenden Beziehung berechnet wird:
| $l = \displaystyle\frac{1}{\sqrt{2} N_A c_m \sigma_0 }$ |
ID:(790, 0)
Gesamtwirkungsquerschnitt für Streuung
Gleichung
Die Gesamtwirkungsquerschnitt für Streuung ($\sigma_0$) ist bei Kollisionen zwischen starren Kugeln gleich einer Funktion von die Radius des Moleküls ($r$):
| $ \sigma_0 = 4 \pi r ^2$ |
ID:(788, 0)
Variation von Muttermalen
Gleichung
Der Variation der Molzahl ($\Delta n$) hängt von die Dichte ($\rho$), der Volumenelement ($\Delta V$) und die Molekülmasse ($M_m$) ab, wie unten dargestellt:
| $ \Delta n = \displaystyle\frac{ \rho \Delta V }{ M_m }$ |
ID:(796, 0)
Schichtvolumen
Gleichung
Der Volumenelement ($\Delta V$) hängt von die Sektion ($S$) und der Schichtdicke ($d$) ab, wie unten gezeigt:
| $ \Delta V = S d $ |
ID:(797, 0)