Utilizador:
Molhando a parede
Storyboard 
Sempre que chove, a umidade relativa atinge valores próximos ou iguais a 100%. Isso significa que o ar está saturado de água, e qualquer superfície absorverá moléculas até formar um filme de água. Esse filme tenderá a escorregar devido à gravidade, começando a "gotejar" pela parede. Além disso, existe um filme de cerca de 120 nm que permanece mesmo após a chuva parar e deve ser removido através do processo de secagem para evitar a formação de mofo, que pode degradar a parede.
ID:(113, 0)
Ar saturado
Conceito
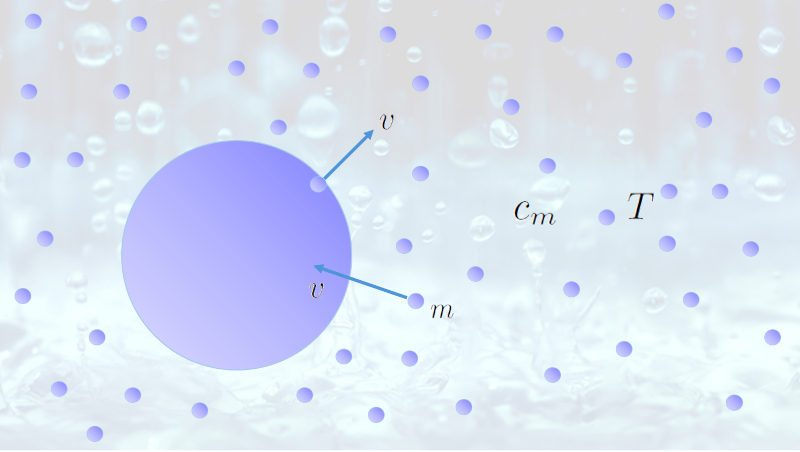
Durante uma chuva, as gotas caem em direção ao solo. Cada gota apresenta uma superfície de água em contato com o ar. As moléculas de água podem se desprender das gotas e se transformar no que chamamos de vapor de água.
Se houver muitas dessas moléculas, a probabilidade não é nula de que elas sejam reabsorvidas pelas gotas. No final, há um equilíbrio entre as moléculas que conseguem escapar e aquelas que são reabsorvidas pelas gotas. Quando o número de moléculas por volume atinge essa situação, dizemos que o ar está saturado de água.
O descrito pode ser modelado obtendo-se o pressão saturada ($p_s$), que depende de o pressão de referência ($p_{ref}$), la calor específico molar de evaporação ($l_m$), o constante de gás universal ($R$) e o temperatura ($T$), através da equação
| $ p_s = p_{ref} e^{- l_m / R T }$ |
que corresponde à pressão do vapor de água para o caso em que o ar está saturado.
Usando as equações dos gases, onde o número de moles ($n$) é expresso por o volume ($V$) e la concentração molar saturada ($c_s$) é expresso por o temperatura ($T$) mediante
| $ p_s = c_s R T $ |
No caso de o ar estar saturado, o umidade relativa ($RH$) é 100%, e assim la concentração molar saturada ($c_s$) é igual a la concentração molar ($c_m$) dado que
| $ RH = \displaystyle\frac{ c_m }{ c_s }$ |
obtemos la concentração molar ($c_m$) do ar durante o evento de chuva.
ID:(798, 0)
Movimento das moléculas de água
Conceito
O pressão saturada ($p_s$) depende de la calor específico molar de evaporação ($l_m$) e o temperatura ($T$), além das constantes o pressão de referência ($p_{ref}$) e o constante de gás universal ($R$):
 $$ |
ID:(799, 0)
Absorção de água na parede
Conceito
Se próximo ao ar saturado com água existe uma superfície, como uma parede, as moléculas de água aderirão a ela. Isso corresponde a um fluxo contínuo enquanto um umidade relativa ($RH$) permanecer igual a 100%. Medidas mostram que a camada cresce enquanto a água flui por gravidade, deixando a borda inferior da parede. No entanto, devido à coesão das moléculas de água, uma camada um espessura da camada ($d$) se forma com uma espessura da ordem de $120 nm$:
o elemento de volume ($\Delta V$) é estimado a partir de o espessura da camada ($d$) e la seção ($S$) através de:
| $ \Delta V = S d $ |
Para uma seção ($S$) de metro quadrado com o espessura da camada ($d$) igual a $120 nm$, temos uma seção ($S$) igual a $1.2e-7 m^2$. O variação do número de moles ($\Delta n$) pode ser calculado com la densidade ($\rho$) igual a $10^3 kg/m^3$, la massa molar ($M_m$) igual a $0.018 kg/ml$ e o elemento de volume ($\Delta V$) com:
| $ \Delta n = \displaystyle\frac{ \rho \Delta V }{ M_m }$ |
resultando em $6.67e-3 mol$. Com um fluxo de vários moles por metro quadrado e por segundo, leva uma fração de segundo para que a parede forme a camada de água.
Qualquer parede que entre em contato com ar saturado se umidifica em frações de segundos
ID:(800, 0)
Modelo
Conceito
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ D = \displaystyle\frac{1}{3} v l $
D = v * l /3
$ \Delta n = \displaystyle\frac{ \rho \Delta V }{ M_m }$
Dn = rho * DV / M_m
$ \Delta V = S d $
DV = S * d
$ j_n = - D \displaystyle\frac{ \Delta c_m }{ \Delta x }$
j_n = - D * Dc_m / Dx
$j_n = \displaystyle\frac{1}{6} c_m v $
j_n = c_m * v /6
$ J_n = \displaystyle\frac{ \Delta c_m }{ \Delta t }$
J_n = Dc_m / Dt
$ J_n = j_n S $
J_n = j_n * S
$l = \displaystyle\frac{1}{\sqrt{2} N_A c_m \sigma_0 }$
l = 1/(sqrt(2)* N_A * c_m * sigma_0 )
$ p = c_m R T $
p = c_m * R * T
$ p_s = c_s R T $
p_s = c_s * R * T
$ p_s = p_{ref} e^{- l_m / R T }$
p_s = p_ref * exp(- l_m /( R * T ))
$ RH = \displaystyle\frac{ c_m }{ c_s }$
RH = c_m / c_s
$ RH = \displaystyle\frac{ p }{ p_s }$
RH = p / p_s
$ \sigma_0 = 4 \pi r ^2$
sigma_0 = 4* pi * r ^2
$v = \sqrt{\displaystyle\frac{8 k_B T }{ \pi m }}$
v = sqrt(8* k_B * T /( pi * m ))
ID:(773, 0)
Pressão saturada
Equação
O pressão saturada ($p_s$) depende de la calor específico molar de evaporação ($l_m$) e o temperatura ($T$), além das constantes o pressão de referência ($p_{ref}$) e o constante de gás universal ($R$):
| $ p_s = p_{ref} e^{- l_m / R T }$ |
ID:(782, 0)
Pressão e concentração molar saturada
Equação
No caso de um gás ideal, o pressão saturada ($p_s$) que satisfaz la concentração molar saturada ($c_s$), o temperatura ($T$) e o constante de gás universal ($R$):
| $ p_s = c_s R T $ |
ID:(781, 0)
Pressão e concentração molar
Equação
No caso de um gás ideal, o pressão ($p$) que satisfaz la concentração molar ($c_m$), o temperatura ($T$) e o constante de gás universal ($R$):
| $ p = c_m R T $ |
ID:(780, 0)
Umidade relativa em função da pressão
Equação
O umidade relativa ($RH$) pode ser calculado usando o pressão ($p$) e o pressão saturada ($p_s$) através da seguinte fórmula:
| $ RH = \displaystyle\frac{ p }{ p_s }$ |
ID:(778, 0)
Umidade relativa em função da concentração
Equação
O umidade relativa ($RH$) pode ser calculado usando la concentração molar ($c_m$) e la concentração molar saturada ($c_s$) através da seguinte fórmula:
| $ RH = \displaystyle\frac{ c_m }{ c_s }$ |
ID:(779, 0)
Fluxo e densidade de fluxo molar
Equação
La fluxo molar ($J_n$) depende de la densidade de fluxo molar ($j_n$) e la seção ($S$), conforme mostrado abaixo:
| $ J_n = j_n S $ |
ID:(784, 0)
Fluxo molar
Equação
La fluxo molar ($J_n$) depende de o diferença de concentração molar ($\Delta c_m$) e o intervalo de tempo ($\Delta t$), conforme mostrado abaixo:
| $ J_n = \displaystyle\frac{ \Delta c_m }{ \Delta t }$ |
ID:(795, 0)
Densidade de fluxo
Equação
La densidade de fluxo molar ($j_n$) depende da concentração de partículas, calculada a partir de la concentração molar ($c_m$) multiplicada por la velocidade das moléculas ($v$) de acordo com a seguinte relação:
| $j_n = \displaystyle\frac{1}{6} c_m v $ |
ID:(791, 0)
Velocidade das moléculas
Equação
La velocidade das moléculas ($v$) pode ser calculado a partir de la constante de Boltzmann ($k_B$), o temperatura ($T$), la pi ($\pi$) e la massa molecular ($m$) usando a seguinte relação:
| $v = \sqrt{\displaystyle\frac{8 k_B T }{ \pi m }}$ |
ID:(789, 0)
Lei de Molar Fick
Equação
La densidade de fluxo molar ($j_n$) depende de la constante de difusão ($D$), que por sua vez depende de o diferença de concentração molar ($\Delta c_m$) e la distância de difusão ($\Delta x$):
| $ j_n = - D \displaystyle\frac{ \Delta c_m }{ \Delta x }$ |
ID:(793, 0)
Coeficiente de difusão
Equação
La constante de difusão ($D$) é modelado como moléculas representadas por esferas que percorrem com la velocidade das moléculas ($v$) Um caminho livre ($l$), da seguinte forma:
| $ D = \displaystyle\frac{1}{3} v l $ |
ID:(786, 0)
Caminho livre
Equação
O caminho livre ($l$) depende da concentração de partículas, calculada a partir de la concentração molar ($c_m$) multiplicada por o número de Avogrado ($N_A$), e de la seção transversal total de espalhamento ($\sigma_0$), de acordo com a seguinte relação:
| $l = \displaystyle\frac{1}{\sqrt{2} N_A c_m \sigma_0 }$ |
ID:(790, 0)
Seção transversal total de espalhamento
Equação
La seção transversal total de espalhamento ($\sigma_0$) é, no caso de colisões entre esferas rígidas, igual a uma função de la raio da molécula ($r$):
| $ \sigma_0 = 4 \pi r ^2$ |
ID:(788, 0)
Variação de toupeiras
Equação
O variação do número de moles ($\Delta n$) depende de la densidade ($\rho$), o elemento de volume ($\Delta V$) e la massa molar ($M_m$), conforme mostrado abaixo:
| $ \Delta n = \displaystyle\frac{ \rho \Delta V }{ M_m }$ |
ID:(796, 0)
Volume da camada
Equação
O elemento de volume ($\Delta V$) depende de la seção ($S$) e o espessura da camada ($d$), conforme mostrado abaixo:
| $ \Delta V = S d $ |
ID:(797, 0)