User:
Wall drying
Storyboard 
The drying of the wall occurs through the evaporation of water and its transport, either by diffusion or airflow. Diffusion is a slow mechanism, as it forms a zone of high humidity on the surface of the wall, hindering further evaporation and dramatically extending the time the wall remains wet.
On the other hand, airflow is a highly efficient mechanism, as the evaporated water is removed by the airflow and replaced by air with lower humidity, which can absorb more water as it evaporates.
ID:(115, 0)
Pressure on the surface
Concept
The pressure on the surface ($p_z$), which acts vertically to the surface:
and is generally smaller than the atmospheric pressure ($p_0$) due to the effects of air displacement from the air density ($\rho_a$) with the wind speed with height ($V_z$).
In this case, we can model it using the Bernoulli equation with its kinetic energy term:
$\displaystyle\frac{1}{2} \rho_a V_Z^2$
This factor is corrected with a factor depending on the shape of the body, the aerodynamic shape factor ($C_a$), and a factor originating from fluctuations due to turbulence vortices, the surface pressure reduction ($q_z$), resulting in:
| $ q_z = \displaystyle\frac{1}{2} \rho_a V_z ^2 C_d C_a$ |
Thus, the pressure on the surface ($p_z$) can be calculated resulting in:
| $ p_z = p_0 - q_z $ |
ID:(768, 0)
Aerodynamic shape factor
Concept
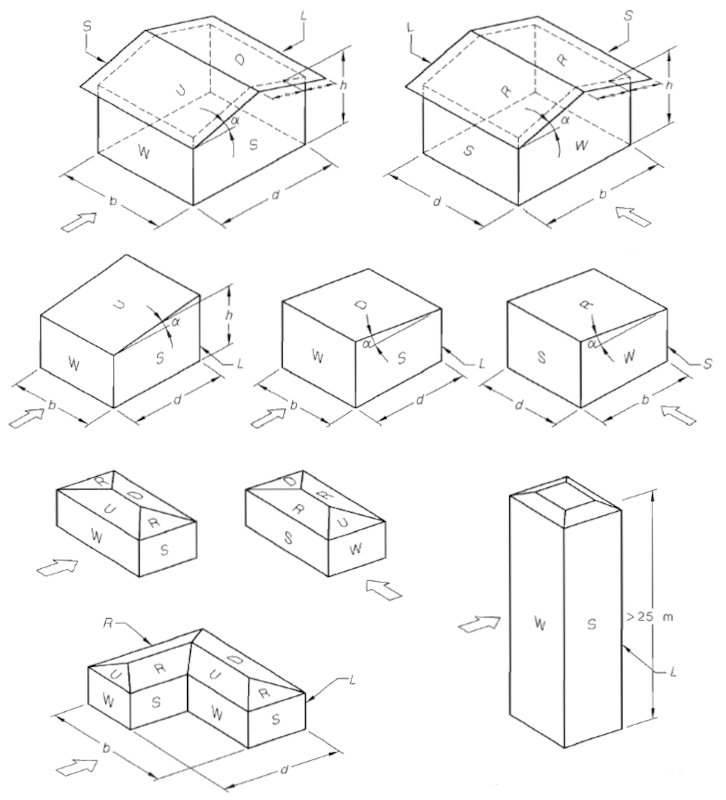
The effect of wind on a structure depends on the direction in which it strikes the surface. If the wind direction is represented by an arrow, we have the following scenarios:
| W | windward (against the wind) |
| S | side |
| L | leeward (with the wind) |
| U | roof slope against the wind |
| R | roof slope with crosswind |
| D | roof slope with the wind |
To better understand these, examples provided in the AS/NZS 1170.2 standard can be consulted:
In summary, the aerodynamic shape factor can be modeled by a factor that depends on the angle between the surface normal and the wind direction. Based on experimental data from various shapes, this factor can be approximated by a shape curve:
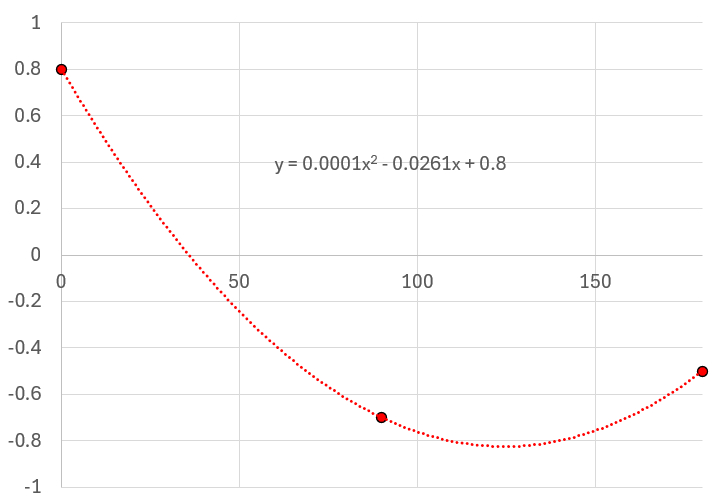
It's important to realize that the function implies the existence of areas of positive pressure as well as areas of negative pressure, which correspond to areas where the wind literally sucks.
ID:(760, 0)
Model
Concept
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ C_a = 0.3445 \theta ^2 - 1.4961 \theta + 0.8$
C_a = 0.3445* theta ^2 - 1.4961* theta + 0.8
$ \Delta p = p_b - p_t $
Dp = p_b - p_t
$ J_V = \displaystyle\frac{ a ^3 b }{12 \eta }\displaystyle\frac{ \Delta p }{ h }$
J_V = a ^3* b * Dp /(12* eta * h)
$ p_b = p_0 - q_b $
p_z = p_0 - q_z
$ p_t = p_0 - q_t $
p_z = p_0 - q_z
$ q_b = \displaystyle\frac{1}{2} \rho_a V_b ^2 C_d C_a$
q_z = rho_a * V_z ^2* C_d * C_a /2
$ q_t = \displaystyle\frac{1}{2} \rho_a V_t ^2 C_d C_a$
q_z = rho_a * V_z ^2* C_d * C_a /2
$ V_b = \displaystyle\frac{2}{5} u \ln\left(\displaystyle\frac{ z_b }{ z_o }\right)$
V_z = 2* u * log( z / z_o )/5
$ V_t = \displaystyle\frac{2}{5} u \ln\left(\displaystyle\frac{ z_t }{ z_o }\right)$
V_z = 2* u * log( z / z_o )/5
ID:(773, 0)
Aerodynamic form factor model
Equation
The aerodynamic shape factor ($C_a$) can be modeled as a function of the wind angle ($\theta$) to estimate the contributions to the pressure from the different surfaces of the object. This model is based on constants derived from measurements taken on various different objects:
| $ C_a = 0.3445 \theta ^2 - 1.4961 \theta + 0.8$ |
ID:(761, 0)
Speed with height (1)
Equation
The wind speed with height ($V_z$) depends on the height above ground ($z$). Typically, it is virtually negligible at the surface and reaches the value reported in meteorological reports at a height of 10 meters. Its variation is influenced by the terrain roughness, expressed by the roughness length ($z_o$), and by the friction speed ($u$), as follows:
| $ V_b = \displaystyle\frac{2}{5} u \ln\left(\displaystyle\frac{ z_b }{ z_o }\right)$ |
| $ V_z = \displaystyle\frac{2}{5} u \ln\left(\displaystyle\frac{ z }{ z_o }\right)$ |
ID:(757, 1)
Speed with height (2)
Equation
The wind speed with height ($V_z$) depends on the height above ground ($z$). Typically, it is virtually negligible at the surface and reaches the value reported in meteorological reports at a height of 10 meters. Its variation is influenced by the terrain roughness, expressed by the roughness length ($z_o$), and by the friction speed ($u$), as follows:
| $ V_t = \displaystyle\frac{2}{5} u \ln\left(\displaystyle\frac{ z_t }{ z_o }\right)$ |
| $ V_z = \displaystyle\frac{2}{5} u \ln\left(\displaystyle\frac{ z }{ z_o }\right)$ |
ID:(757, 2)
Reduction of pressure on the surface (1)
Equation
The surface pressure reduction ($q_z$) is the pressure per unit area by which it decreases on the surface of the body. It is modeled as a modification of the Bernoulli's principle, characterized by the air density ($\rho_a$) and the wind speed with height ($V_z$), correcting for dynamics with the dynamic response factor ($C_d$), and geometry with the aerodynamic shape factor ($C_a$):
| $ q_b = \displaystyle\frac{1}{2} \rho_a V_b ^2 C_d C_a$ |
| $ q_z = \displaystyle\frac{1}{2} \rho_a V_z ^2 C_d C_a$ |
ID:(759, 1)
Reduction of pressure on the surface (2)
Equation
The surface pressure reduction ($q_z$) is the pressure per unit area by which it decreases on the surface of the body. It is modeled as a modification of the Bernoulli's principle, characterized by the air density ($\rho_a$) and the wind speed with height ($V_z$), correcting for dynamics with the dynamic response factor ($C_d$), and geometry with the aerodynamic shape factor ($C_a$):
| $ q_t = \displaystyle\frac{1}{2} \rho_a V_t ^2 C_d C_a$ |
| $ q_z = \displaystyle\frac{1}{2} \rho_a V_z ^2 C_d C_a$ |
ID:(759, 2)
Pressure on the surface of a body (1)
Equation
The pressure on the surface ($p_z$) is equal to the atmospheric pressure ($p_0$) reduced by the surface pressure reduction ($q_z$):
| $ p_b = p_0 - q_b $ |
| $ p_z = p_0 - q_z $ |
ID:(776, 1)
Pressure on the surface of a body (2)
Equation
The pressure on the surface ($p_z$) is equal to the atmospheric pressure ($p_0$) reduced by the surface pressure reduction ($q_z$):
| $ p_t = p_0 - q_t $ |
| $ p_z = p_0 - q_z $ |
ID:(776, 2)
Pressure difference between wall edges
Equation
The pressure difference between bottom and top edge ($\Delta p$) is calculated from the difference of the pressure on the bottom edge ($p_b$) and the pressure on the top edge ($p_t$):
| $ \Delta p = p_b - p_t $ |
ID:(775, 0)
Water vapor flow
Equation
The estimation of the pressure on the top edge ($p_t$) is based on the moisture moving through the space between the wall and the cladding, driven by the pressure difference between bottom and top edge ($\Delta p$). Assuming that the distance SIP and cladding ($a$), the distance between slats ($b$), the vertical wall height ($h$), and the viscosity ($\eta$):
| $ J_V = \displaystyle\frac{ a ^3 b }{12 \eta }\displaystyle\frac{ \Delta p }{ h }$ |
ID:(774, 0)