Utilisateur:
Méthode de modélisation
Storyboard 
Pour réaliser diverses analyses, il est essentiel de disposer d'un modèle simplifié de la maison. À cet effet, un système de coordonnées initial est établi comme référence pour définir tous les points clés. À l'aide de ces points, il est possible de définir des plans pour les murs, les plafonds et les planchers. De plus, il est possible d'incorporer des portes et des fenêtres dans les murs selon les besoins.
ID:(92, 0)
Modèle de base
Description
Le modèle de base se compose d'une série de points correspondant aux coins des surfaces. Cette approche de modélisation est similaire à la manière dont, par le passé, des maquettes de maisons, de bateaux et d'avions étaient assemblées en découpant des feuilles de carton et en les assemblant:
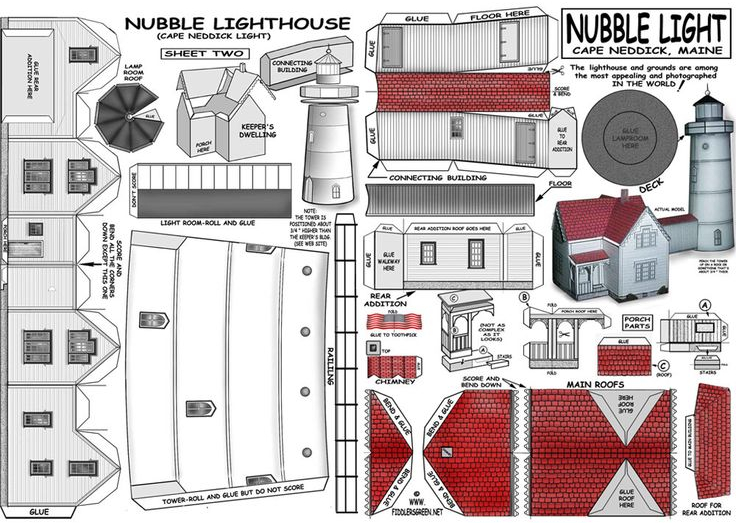
Dans notre cas, nous identifions des points aux coins des murs, des plafonds et des sols. Des groupes de ces points se combinent pour former ces surfaces, comme dans cet exemple montrant le mur avant de la maison du phare:
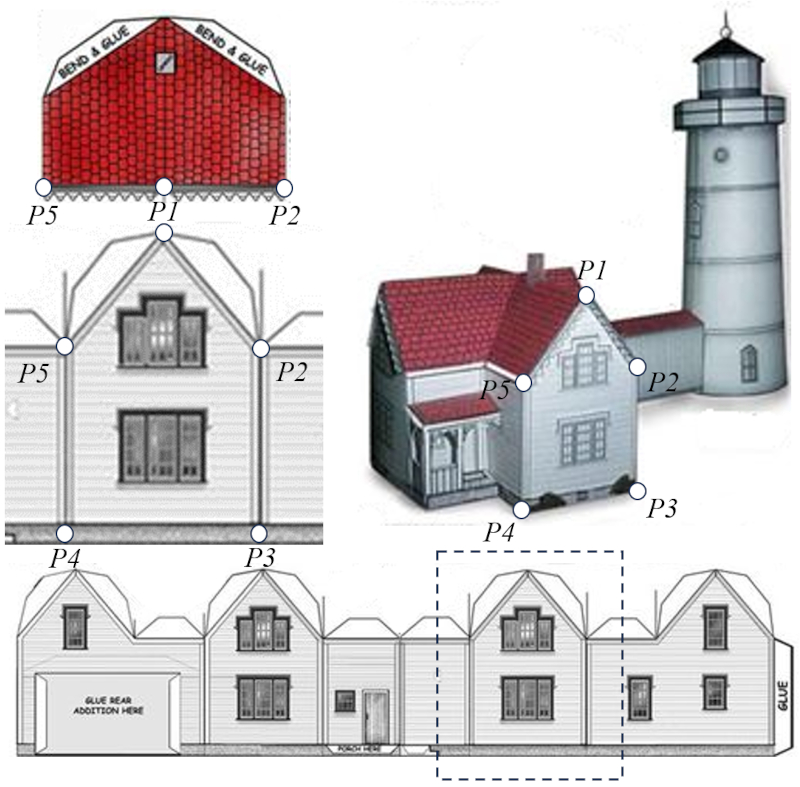
Les points de la façade sont également des points des murs latéraux, des plafonds et du sol, bien que cela ne soit pas visible dans ce diagramme.
ID:(438, 0)
Coordonnées
Description
Pour commencer, il est essentiel de définir un système de coordonnées à travers lequel tous les points et par la suite toutes les surfaces seront définis. Étant donné que le système de coordonnées peut être ajusté ultérieurement, et donc l'ensemble de la conception, il n'est pas crucial de fixer une orientation en fonction de l'orientation finale de la maison. L'objectif est plutôt d'établir un système pratique pour définir la structure.
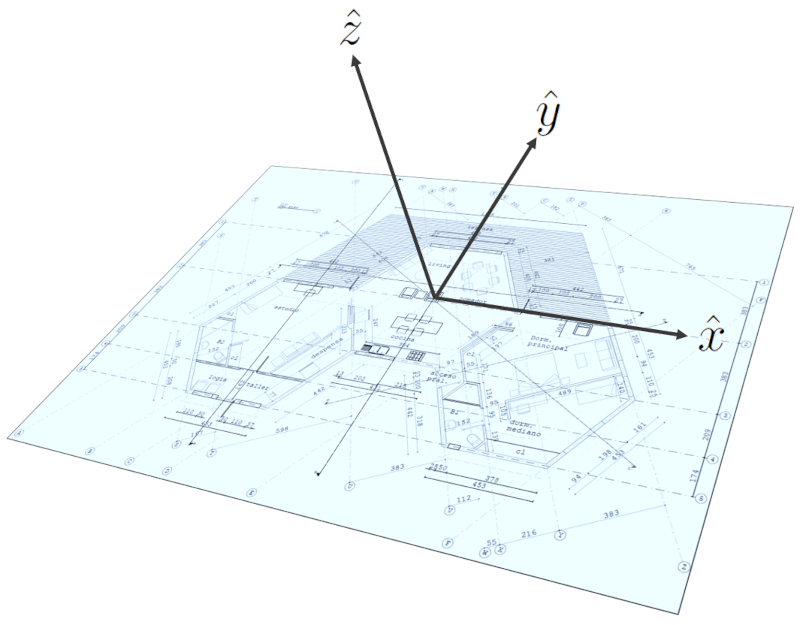
Dans le cas de ce projet, nous avons utilisé un point au sol comme origine, situé au centre du module abritant le salon, la salle à manger et la cuisine. L'orientation a été choisie de manière à ce que l'axe z suive les lignes verticales, l'axe y se situe entre le centre de l'hexagone et le point médian du bord de la fenêtre principale (c'est-à-dire le long de la ligne qui sépare le salon de la salle à manger), et enfin, l'axe x est positionné de manière orthogonale le long de la ligne allant du devant du studio à celui de la chambre.
ID:(588, 0)
Points
Image
Une fois que le système de coordonnées a été défini, nous pouvons procéder à la définition de tous les points qui représentent les différentes surfaces. Pour ce faire, nous devons spécifier les distances le long des axes $\hat{x}$, $\hat{y}$ et $\hat{z}$ à partir de l'origine associée au système.
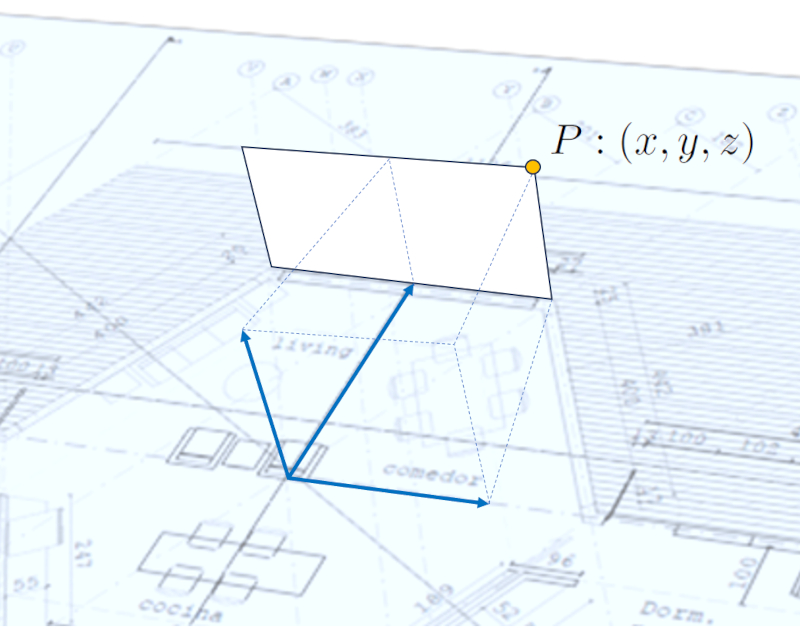
De plus, pour faciliter les définitions de surface, il est pratique d'établir un code ou un nom pour chaque point. Cela peut inclure de la logique, comme indiquer avec un numéro ou une lettre initiale le niveau des points, suivi d'un séparateur tel qu'un point, et d'un numéro consécutif. Par exemple, '0' pour le niveau du sol, '1' pour le niveau du plafond, de sorte que le cinquième point au premier niveau serait désigné par $P_{0.5}$.
ID:(589, 0)
Vecteurs
Équation
Avec deux points, vous pouvez définir un vecteur en soustrayant les coordonnées d'un point des coordonnées de l'autre.
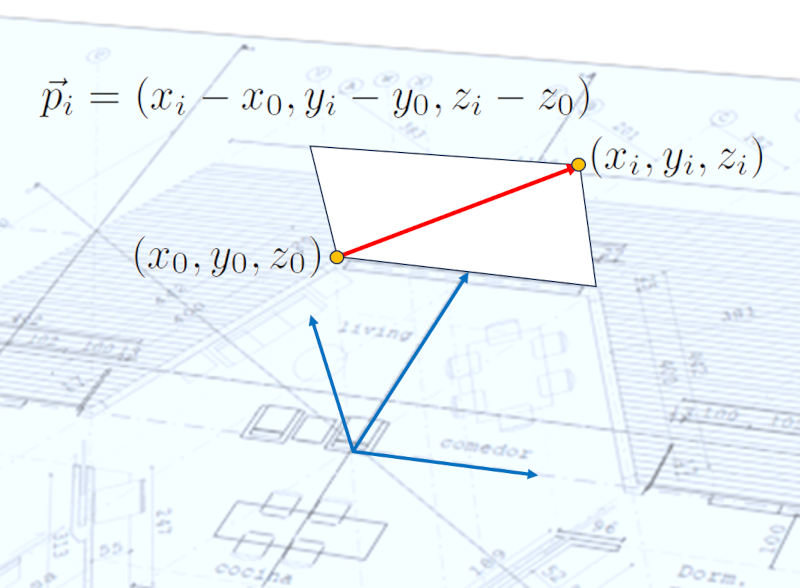
Ce concept est exprimé à travers les composantes calculées de chaque différence et est représenté par une lettre avec une flèche au-dessus :
 $ \vec{p}_i = (p_{i,x} - p_{0,x},p_{i,y} - p_{0,y},p_{i,z} - p_{0,z})$ |
ID:(595, 0)
Longueur du vecteur
Équation
Avec deux points, vous pouvez définir un vecteur en soustrayant les coordonnées d'un point des coordonnées de l'autre. Par conséquent, chaque composante du vecteur correspond à un côté d'un prisme. Si vous observez les points dans un plan, la figure géométrique se réduit à un triangle :
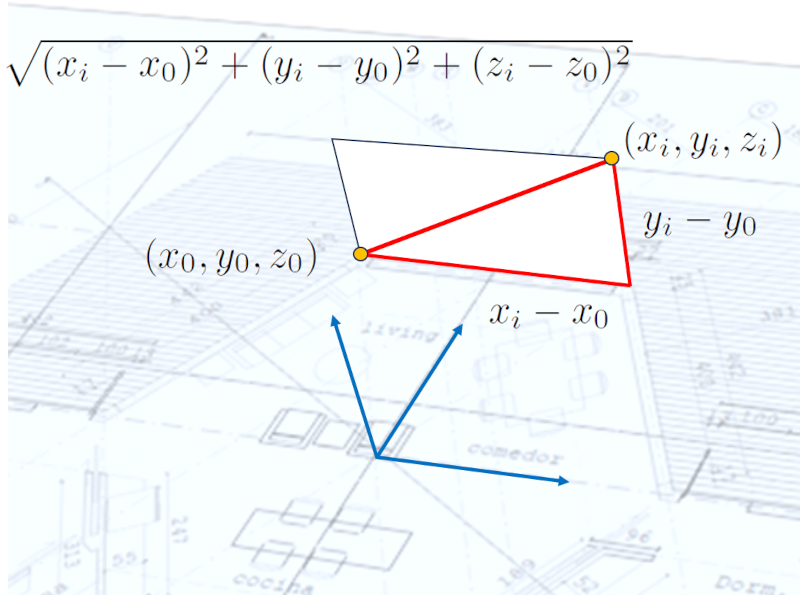
En général, la longueur du vecteur peut être calculée à l'aide du théorème de Pythagore, et le résultat est la magnitude du vecteur :
| $ \mid\vec{p}_i\mid = \sqrt{(p_{i,x} - p_{0,x})^2+(p_{i,y} - p_{0,y})^2+(p_{i,z} - p_{0,z})^2}$ |
Cela s'appelle la magnitude du vecteur.
ID:(596, 0)
Surfaces
Description
Chaque surface est composée d'au moins trois points, ce qui correspond à un triangle. Un rectangle est composé de quatre points, tandis qu'une forme plus complexe comme un hexagone utilise six points.
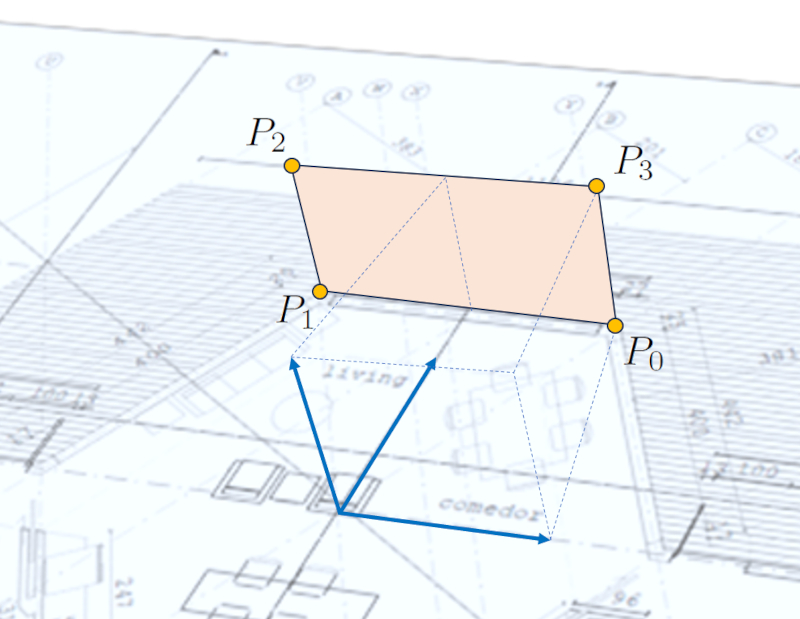
Pour définir une surface, il est nécessaire de spécifier les points qui la composent dans l'ordre où ils doivent être reliés. De plus, vous pouvez attribuer un nom à chaque surface pour faciliter son identification ultérieure.
Pour éviter des problèmes, il est important de garder à l'esprit que :
Il est essentiel de se rappeler que tous les autres vecteurs unitaires qui peuvent être définis avec les points restants et la même origine doivent être dans le même plan que celui défini par le premier et le dernier vecteur. Sinon, la surface ne sera pas plate.
ID:(590, 0)
Versor
Équation
Pour calculer les flux lumineux dans les calculs d'éclairage et de chauffage solaire, il est nécessaire de travailler avec la direction normale aux surfaces telles que les fenêtres, les murs et les plafonds. Pour obtenir cette direction, nous devons normaliser le vecteur correspondant, c'est-à-dire le diviser par sa longueur, de manière à ce que sa longueur soit toujours égale à une unité, quelle que soit la direction dans laquelle il pointe.
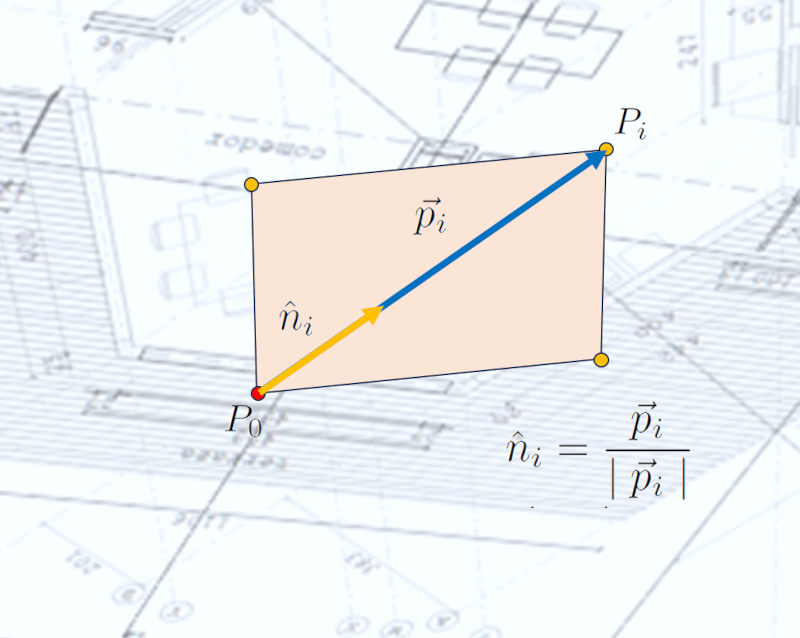
Par conséquent, le vecteur unitaire (indiqué par un chapeau au lieu d'une flèche, par exemple $\hat{x}$) est défini comme le vecteur vers le point $i$-ème $\vec{p}_i$ divisé par sa magnitude $\mid\vec{p}_i\mid$ :
| $ \hat{n}_i = \displaystyle\frac{\vec{p}_i}{\mid\vec{p}_i\mid}$ |
ID:(597, 0)
Superficie depuis la surface
Équation
L'aire du parallélépipède généré par deux vecteurs peut être directement calculée à partir de la magnitude du produit vectoriel de ces vecteurs. Par conséquent, si vous souhaitez calculer l'aire entre des ensembles successifs de vecteurs, vous pouvez le faire de la manière suivante : la première aire est calculée entre le vecteur $\vec{p}_2$ et le vecteur $\vec{p}_1$, la deuxième entre le vecteur $\vec{p}_3$ et le vecteur $\vec{p}_2$, et ainsi de suite. Cela peut être mieux visualisé avec un exemple de quatre points :
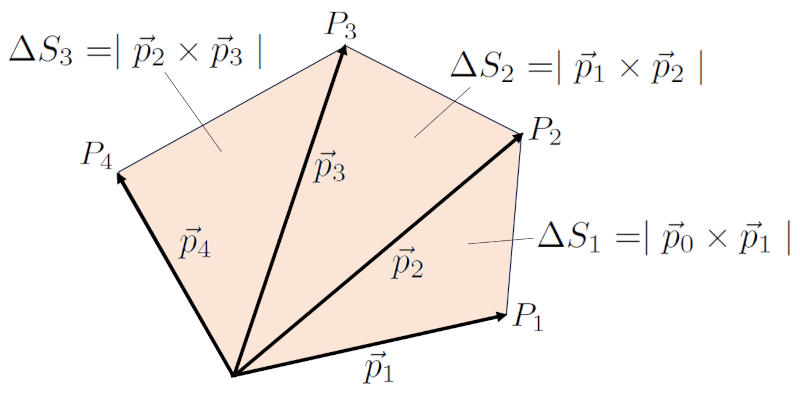
En général, l'aire totale se calcule de la manière suivante :
| $ S = \displaystyle\sum_i \mid \vec{p}_{i+1} \times \vec{p}_i \mid$ |
ID:(594, 0)
Versor normal à la surface
Équation
Si nous prenons le premier point $P_0$ de la séquence de points définissant une surface comme origine, le deuxième point $P_1$ pour définir le premier vecteur unitaire $\hat{n}_1$, et le dernier point $P_N$ pour définir le deuxième vecteur unitaire $\hat{n}_N$, nous pouvons définir le vecteur unitaire normal à la surface comme suit :
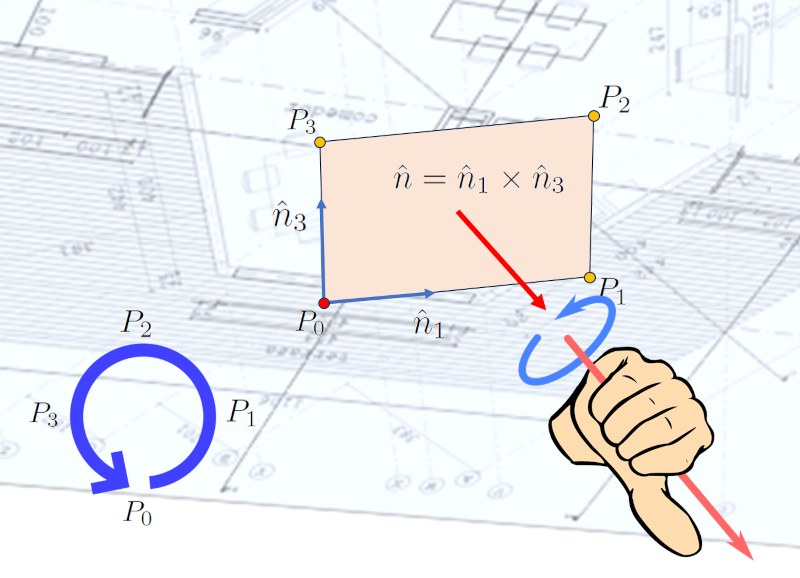
Étant donné que les vecteurs unitaires sont, par définition, normalisés, le produit vectoriel est également normalisé, ce qui signifie que le résultat reflète une direction.
Pour effectuer le calcul, nous pouvons travailler avec les vecteurs unitaires $(n_{1,x}, n_{1,y}, n_{1,z})$ et $(n_{N,x}, n_{N,y}, n_{N,z})$. Nous pouvons utiliser l'équation suivante :
$\hat{n}_1\times\hat{n}_N=(n_{1,y}n_{N,z}-n_{1,z}n_{N,y},n_{1,z}n_{N,x}-n_{1,x}n_{N,z},n_{1,x}n_{N,y}-n_{1,y}n_{N,x})$
ID:(591, 0)
Fenêtres et portes
Image
Pour la définition des portes et des fenêtres, nous travaillons avec un système de coordonnées locales défini par les vecteurs unitaires qui ont été utilisés pour calculer le vecteur unitaire normal, à savoir $\hat{n}_1$ et $\hat{n}_N$. Nous travaillons sur la surface où le vecteur unitaire normal est positif. Nous commençons par définir le coin inférieur gauche de la porte ou de la fenêtre. Ensuite, nous spécifions sa largeur et sa hauteur.
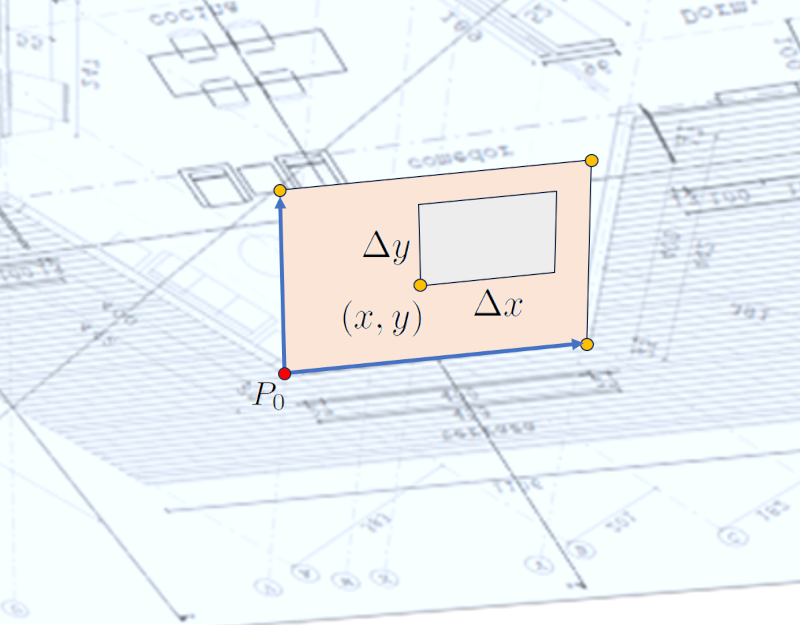
Chaque fenêtre et porte est définie individuellement.
ID:(592, 0)
Rotation des maisons
Image
Une fois que les points, les surfaces (murs, sols et plafonds), les fenêtres et les portes ont été définis, il est possible de faire pivoter la conception. Cela est dû au fait que, dans la définition initiale, il est pratique d'utiliser un système de coordonnées le plus simple possible, qui peut ne pas nécessairement être aligné avec le nord en tant qu'axe $\hat{y}$ et l'est en tant qu'axe $\hat{x}$. Cependant, la rotation, généralement autour de l'axe vertical $\hat{z}$, permet d'exprimer l'ensemble de la conception dans un système de coordonnées plus pratique spatialement :
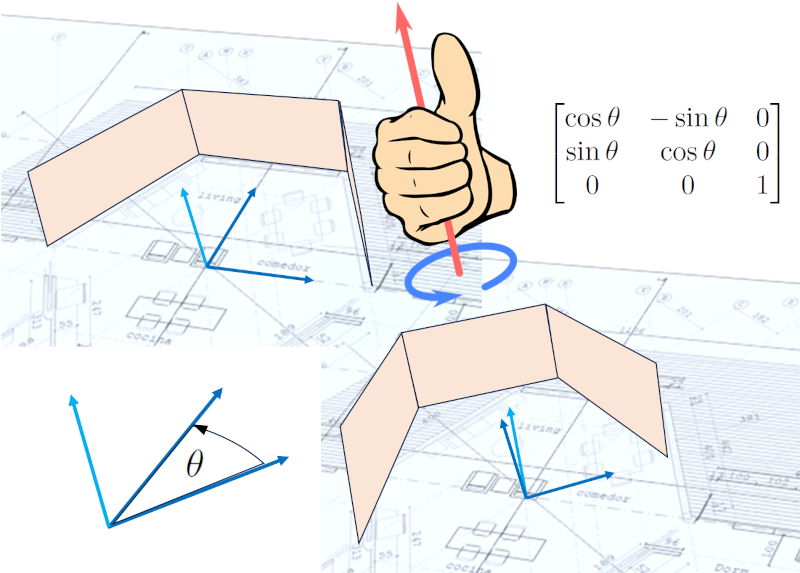
La rotation déplace tous les points et, par conséquent, tous les vecteurs et vecteurs unitaires qui ont été calculés. Cela est important car cela permet d'étudier comment la lumière interagit avec la structure.
ID:(593, 0)