Storyboard

Para realizar diversas análises, é fundamental contar com um modelo simplificado da casa. Para isso, inicialmente estabelecemos um sistema de coordenadas que serve como referência para definir todos os pontos-chave. Utilizando esses pontos, é possível estabelecer planos para as paredes, os tetos e os pisos. Além disso, é possível incorporar portas e janelas nas paredes conforme necessário.

>Modelo

ID:(92, 0)

Descrição

>Top

O modelo básico consiste em uma série de pontos que correspondem às esquinas das superfícies. Essa abordagem de modelagem é semelhante à forma como, no passado, modelos de casas, barcos e aviões eram montados recortando folhas de papelão e montando-as:

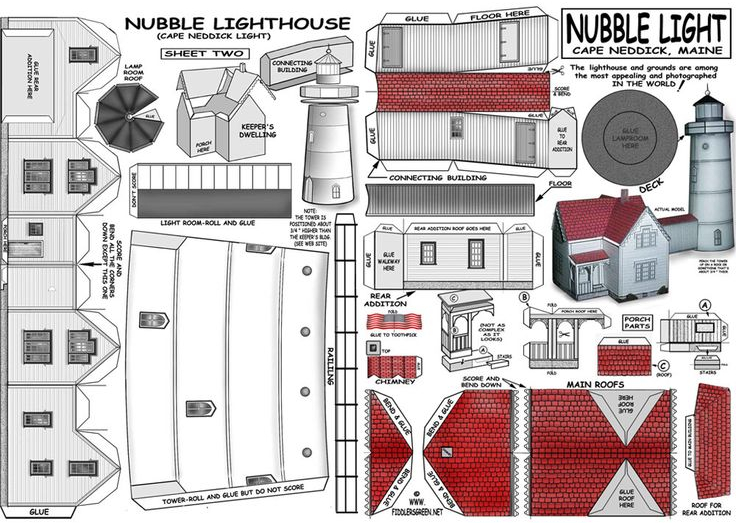
No nosso caso, identificamos pontos nas esquinas das paredes, tetos e pisos. Grupos desses pontos se unem para formar essas superfícies, como neste exemplo que mostra a parede frontal da casa do farol:

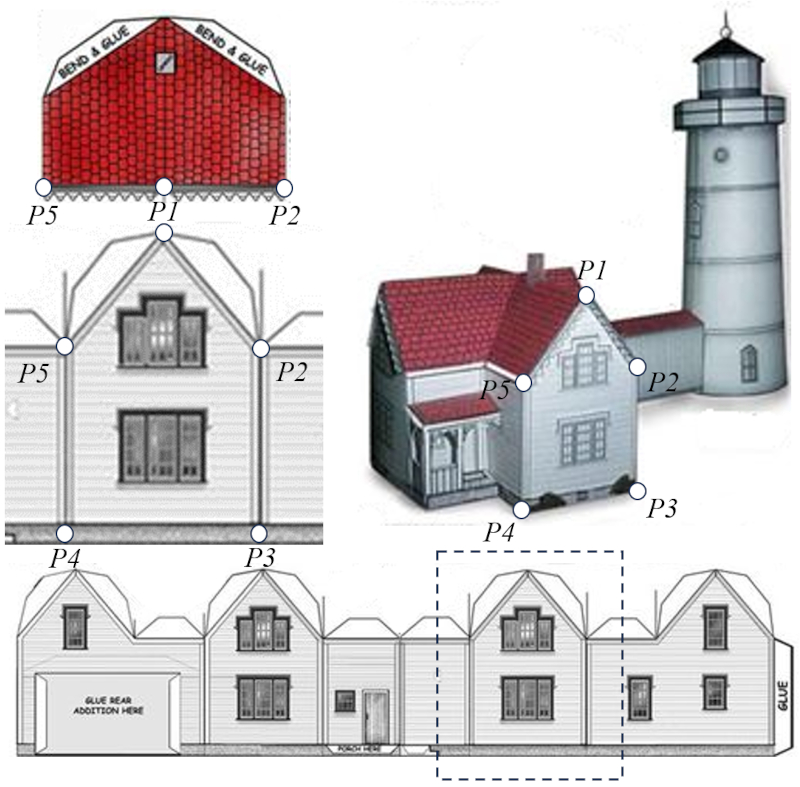
Os pontos na fachada também são pontos nas paredes laterais, nos tetos e no chão, embora isso não seja visível neste diagrama.

ID:(438, 0)

Descrição

>Top

Para começar, é fundamental definir um sistema de coordenadas por meio do qual todos os pontos e, posteriormente, as superfícies serão definidos. Uma vez que o sistema de coordenadas pode ser ajustado posteriormente, e, com isso, o design como um todo, não é crucial fixar uma orientação com base na disposição final da casa. Em vez disso, o objetivo é estabelecer um sistema que seja conveniente para definir a estrutura.

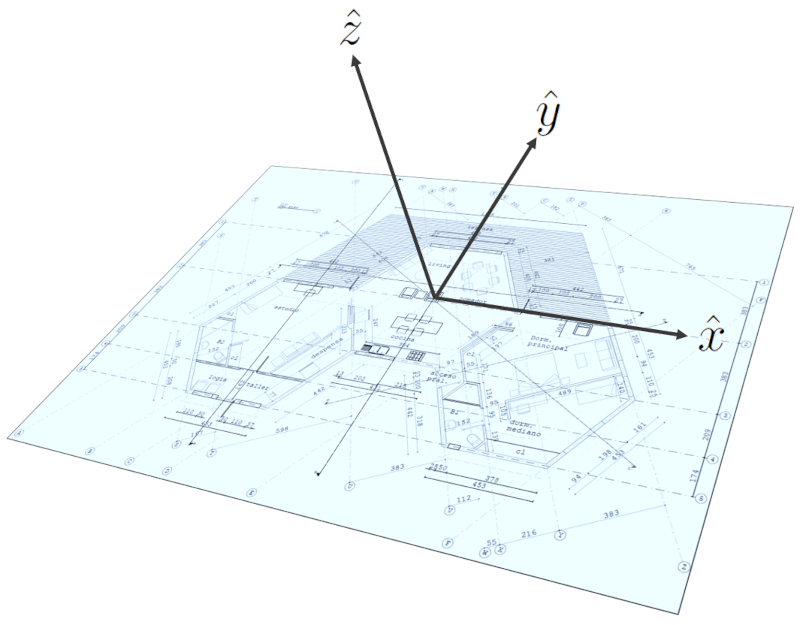
No caso deste projeto, utilizamos um ponto no solo como origem, localizado no centro do módulo que abriga a sala de estar, a área de jantar e a cozinha. A orientação foi definida de forma que o eixo z se estenda ao longo das linhas verticais, o eixo y esteja entre o centro do hexágono e o ponto médio da borda da janela principal (ou seja, ao longo da linha que separa a sala de estar da área de jantar) e, finalmente, o eixo x seja posicionado de forma ortogonal na linha que vai desde a frente do estúdio até o do quarto.

ID:(588, 0)

Imagem

>Top

Uma vez que o sistema de coordenadas tenha sido definido, podemos proceder à definição de todos os pontos que representam as diferentes superfícies. Para fazer isso, é necessário especificar as distâncias ao longo dos eixos $\hat{x}$, $\hat{y}$ e $\hat{z}$ a partir da origem associada ao sistema.

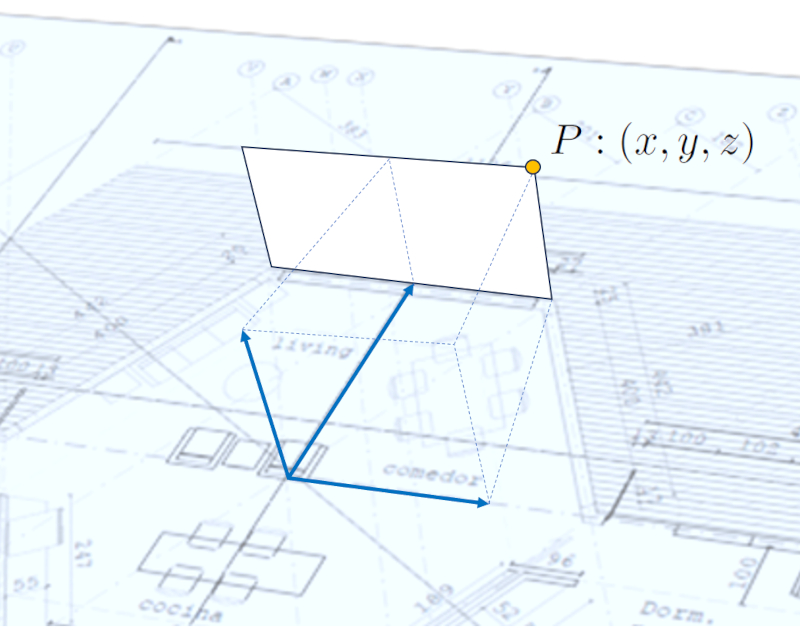
Além disso, para facilitar as definições das superfícies, é conveniente estabelecer algum código ou nome para cada ponto. Isso pode incluir lógica, como indicar com um número ou letra inicial o nível dos pontos, seguido de um separador como um ponto, e um número sequencial. Por exemplo, '0' para o nível do solo, '1' para o nível do teto, de modo que o quinto ponto no primeiro nível seria denominado $P_{0.5}$.

ID:(589, 0)

Equação

>Top, >Modelo

Com dois pontos, você pode definir um vetor subtraindo as coordenadas de um ponto das coordenadas do outro.



Esse conceito é expresso por meio das componentes calculadas de cada diferença e é representado por uma letra com uma seta acima dela:

$ \vec{p}_i = (p_{i,x} - p_{0,x},p_{i,y} - p_{0,y},p_{i,z} - p_{0,z})$

Condições

Variáveis

Relação

ID:(595, 0)

Equação

>Top, >Modelo

Com dois pontos, você pode definir um vetor subtraindo as coordenadas de um ponto das coordenadas do outro. Portanto, cada componente do vetor corresponde a um lado de um prisma. Se você observar os pontos em um plano, a figura geométrica se reduz a um triângulo:

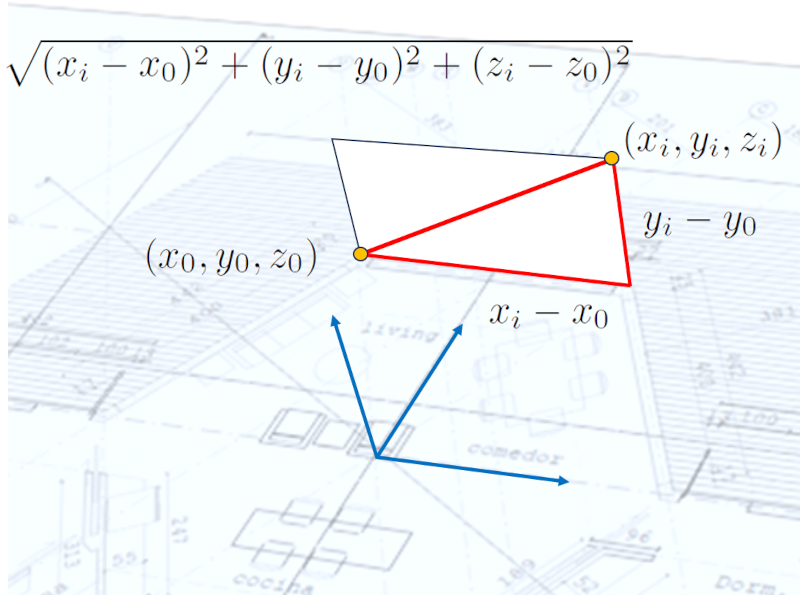
Em geral, o comprimento do vetor pode ser calculado usando o teorema de Pitágoras, e o resultado é a magnitude do vetor:

$ \mid\vec{p}_i\mid = \sqrt{(p_{i,x} - p_{0,x})^2+(p_{i,y} - p_{0,y})^2+(p_{i,z} - p_{0,z})^2}$

Condições

Variáveis

Relação

Isso é chamado de magnitude do vetor.

ID:(596, 0)

Descrição

>Top

Toda superfície é composta por pelo menos três pontos, o que corresponde a um triângulo. Um retângulo é composto por quatro pontos, enquanto uma forma mais complexa, como um hexágono, utiliza seis pontos.



Para definir uma superfície, é necessário especificar os pontos que a compõem na ordem em que devem ser conectados. Além disso, você pode atribuir um nome a cada superfície para facilitar a identificação posterior.

Para evitar problemas, é importante ter em mente que:

É crucial lembrar que todos os outros vetores unitários que podem ser definidos com os pontos restantes e a mesma origem devem estar no mesmo plano definido pelo primeiro e pelo último vetor. Caso contrário, a superfície não será plana.

ID:(590, 0)

Equação

>Top, >Modelo

Para calcular os fluxos de luz nos cálculos de iluminação e aquecimento solar, é necessário trabalhar com a direção normal às superfícies, como janelas, paredes e tetos. Para obter essa direção, precisamos normalizar o vetor correspondente, ou seja, dividi-lo pelo seu comprimento, de forma que seu comprimento seja sempre igual a uma unidade, independentemente da direção para a qual aponta.

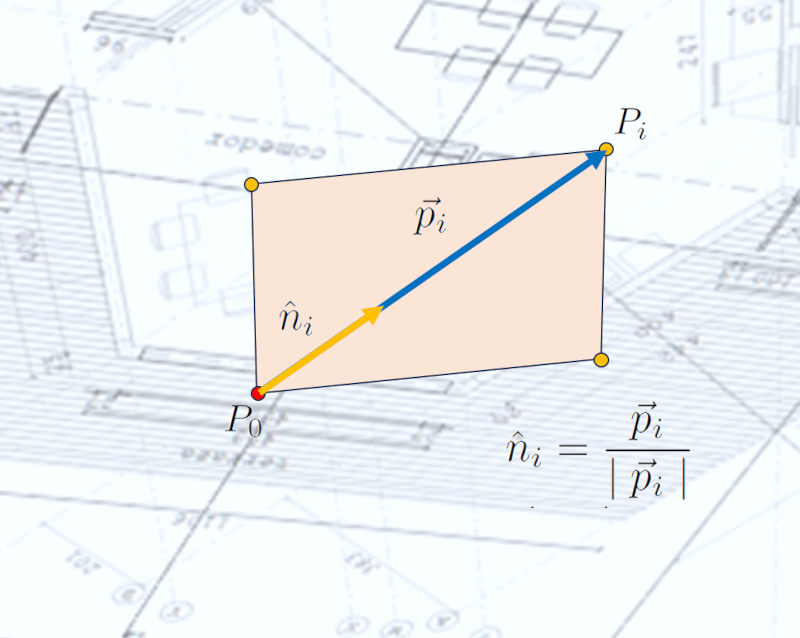
Portanto, o vetor unitário (indicado com um chapéu em vez de uma seta, por exemplo, $\hat{x}$) é definido como o vetor para o ponto $i$-ésimo $\vec{p}_i$ dividido pela sua magnitude $\mid\vec{p}_i\mid$:

$ \hat{n}_i = \displaystyle\frac{\vec{p}_i}{\mid\vec{p}_i\mid}$

Condições

Variáveis

Relação

ID:(597, 0)

Equação

>Top, >Modelo

A área do paralelepípedo gerado por dois vetores pode ser calculada diretamente a partir da magnitude do produto cruz desses vetores. Portanto, se você deseja calcular a área entre conjuntos sucessivos de vetores, pode fazê-lo da seguinte forma: a primeira área é calculada entre o vetor $\vec{p}_2$ e o vetor $\vec{p}_1$, a segunda entre o vetor $\vec{p}_3$ e o vetor $\vec{p}_2$, e assim por diante. Isso pode ser visualizado melhor com um exemplo de quatro pontos:

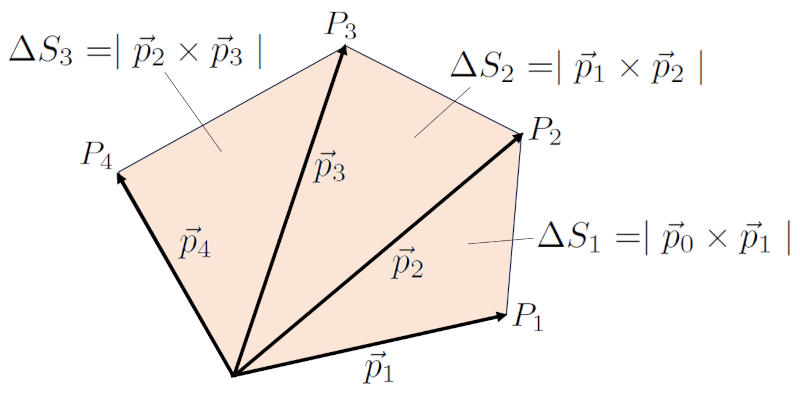
Em geral, a área total é calculada da seguinte forma:

$ S = \displaystyle\sum_i \mid \vec{p}_{i+1} \times \vec{p}_i \mid$

Condições

Variáveis

Relação

ID:(594, 0)

Equação

>Top, >Modelo

Se tomarmos o primeiro ponto $P_0$ da sequência de pontos que define uma superfície como a origem, o segundo ponto $P_1$ para definir o primeiro vetor unitário $\hat{n}_1$, e o último ponto $P_N$ para definir o segundo vetor unitário $\hat{n}_N$, podemos definir o vetor unitário normal à superfície da seguinte maneira:



Como os vetores unitários são, por definição, normalizados, o produto cruzado também é normalizado, o que significa que o resultado reflete uma direção.

Para realizar o cálculo, podemos trabalhar com os vetores unitários $(n_{1,x}, n_{1,y}, n_{1,z})$ e $(n_{N,x}, n_{N,y}, n_{N,z})$. Podemos usar a seguinte equação:

$\hat{n}_1\times\hat{n}_N=(n_{1,y}n_{N,z}-n_{1,z}n_{N,y},n_{1,z}n_{N,x}-n_{1,x}n_{N,z},n_{1,x}n_{N,y}-n_{1,y}n_{N,x})$

ID:(591, 0)

Imagem

>Top

Para a definição de portas e janelas, trabalhamos com um sistema de coordenadas locais definido pelos vetores unitários que foram usados para calcular o vetor unitário normal, que são $\hat{n}_1$ e $\hat{n}_N$. Trabalhamos na superfície onde o vetor unitário normal é positivo. Começamos por definir o canto inferior esquerdo da porta ou janela. Em seguida, especificamos a largura e a altura dela.

Cada janela e porta é definida individualmente.

ID:(592, 0)

Imagem

>Top

Depois que os pontos, superfícies (paredes, pisos e tetos), janelas e portas foram definidos, é possível rotacionar o design. Isso ocorre porque, na definição inicial, é conveniente usar um sistema de coordenadas o mais simples possível, que pode não se alinhar necessariamente com o norte como o eixo $\hat{y}$ e leste como o eixo $\hat{x}$. No entanto, a rotação, normalmente em torno do eixo vertical $\hat{z}$, permite expressar todo o design em um sistema de coordenadas que seja espacialmente mais conveniente:

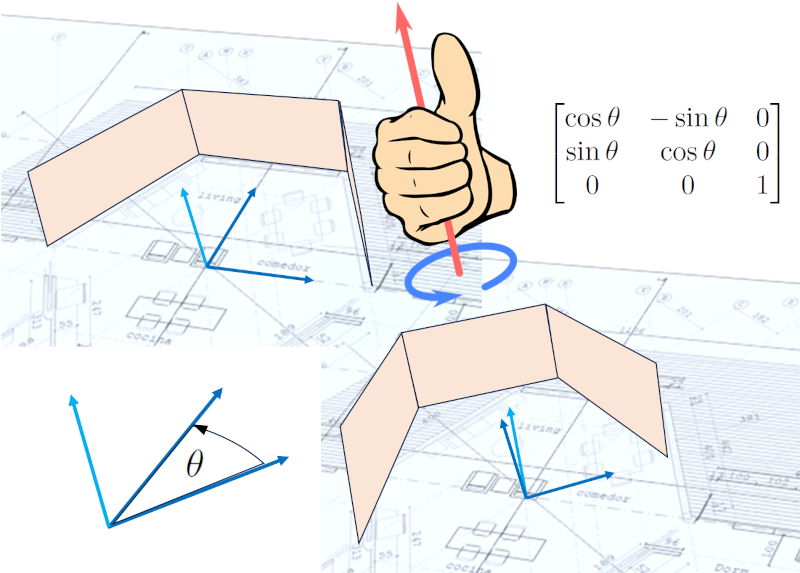
A rotação desloca todos os pontos e, consequentemente, todos os vetores e vetores unitários que foram calculados. Isso é importante porque permite estudar como a luz interage com a estrutura.

ID:(593, 0)